
【题目】如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点. 
(1)求证:VD∥平面EAC;
(2)求二面角A﹣VB﹣D的余弦值.
【答案】
(1)证明:由正视图可知:平面VAB⊥平面ABCD
连接BD交AC于O点,连接EO,由已知得BO=OD,VE=EB
∴VD∥EO
又VD平面EAC,EO平面EAC
∴VD∥平面EAC;
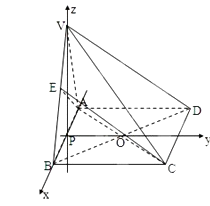
(2)解:设AB的中点为P,则VP⊥平面ABCD,建立如图所示的坐标系,
则 ![]() =(0,1,0)
=(0,1,0)
设平面VBD的法向量为 ![]()
∵ ![]()
∴由 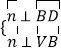 ,可得
,可得 ![]() ,∴可取
,∴可取 ![]() =(
=( ![]() ,
, ![]() ,1)
,1)
∴二面角A﹣VB﹣D的余弦值cosθ= ![]() =
= ![]()
【解析】(1)欲证VD∥平面EAC,根据直线与平面平行的判定定理可知只需证VD与平面EAC内一直线平行即可,而连接BD交AC于O点,连接EO,由已知易得VD∥EO,VD平面EAC,EO平面EAC,满足定理条件;(2)设AB的中点为P,则VP⊥平面ABCD,建立坐标系,利用向量的夹角公式,可求二面角A﹣VB﹣D的余弦值.


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处的切线平行于直线
处的切线平行于直线![]() ,求实数a的值;
,求实数a的值;
(Ⅱ)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(Ⅲ)在(Ⅰ)的条件下,若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],若低于60分的人数是15人,则该班的学生人数是( ) 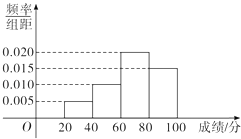
A.45
B.50
C.55
D.60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系内,已知A(1,a),B(﹣5,﹣3),C(4,0);
(1)当a∈( ![]() ,3)时,求直线AC的倾斜角α的取值范围;
,3)时,求直线AC的倾斜角α的取值范围;
(2)当a=2时,求△ABC的BC边上的高AH所在直线方程l.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x+2 ![]() sinxcosx﹣sin2x.
sinxcosx﹣sin2x.
(1)求f(x)的最小正周期和值域;
(2)在△ABC中,角A,B,C所对的边分别是a,b,c,若 ![]() 且a2=bc,试判断△ABC的形状.
且a2=bc,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a∈R,则“关于x的方程x2+ax+1=0无实根”是“z=(2a﹣1)+(a﹣1)i(其中i表示虚数单位)在复平面上对应的点位于第四象限”的( )
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既非充分又非必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com