
分析 (Ⅰ)化简可得数列{an}的奇数项构成以1为首项,2为公差的等差数列,数列{an}的偶数项构成以2为首项,3为公比的等比数列,从而写出通项公式;
(Ⅱ)分类讨论即方程的解;
(Ⅲ)化简S2m=1+2+3+6+…+2m-1+2•3m-1=3m-1+m2,S2m-1=3m-1-1+m2,从而可得$\frac{{{S_{2m}}}}{{{S_{2m-1}}}}$=1+$\frac{2}{1+\frac{{m}^{2}-1}{{3}^{m-1}}}$,从而讨论求值.
解答 解:(Ⅰ)∵${a_1}=1,{a_2}=2,{a_{2n+1}}={a_{2n-1}}+2,{a_{2n+2}}=3{a_{2n}},(n∈{N^*})$,
∴数列{an}的奇数项构成以1为首项,2为公差的等差数列,
数列{an}的偶数项构成以2为首项,3为公比的等比数列,
故an=$\left\{\begin{array}{l}{n,n为奇数}\\{2•{\sqrt{3}}^{n-2},n为偶数}\end{array}\right.$;
(Ⅱ)若m为奇数,则amam+1=m•2•$\sqrt{3}$m-1=m+2,
无解;
若m为偶数,则amam+1=(m+1)2•$\sqrt{3}$m-2=2•$\sqrt{3}$m,
即$\frac{2(m+1)}{3}$=2,
解得,m=2;
综上所述,m=2;
(Ⅲ)由题意知,S2m=1+2+3+6+…+2m-1+2•3m-1
=(1+3+5+…+2m-1)+(2+6+18+…+2•3m-1)
=$\frac{1+2m-1}{2}$•m+$\frac{2(1-{3}^{m})}{1-3}$
=3m-1+m2,
S2m-1=1+2+3+6+…+2m-1
=(1+3+5+…+2m-1)+(2+6+18+…+2•3m-2)
=$\frac{1+2m-1}{2}$•m+$\frac{2(1-{3}^{m})}{1-3}$-2•3m-1
=3m-1-1+m2,
故$\frac{{{S_{2m}}}}{{{S_{2m-1}}}}$=$\frac{{3}^{m}+{m}^{2}-1}{{3}^{m-1}+{m}^{2}-1}$=1+$\frac{2}{1+\frac{{m}^{2}-1}{{3}^{m-1}}}$,
若m=1,则$\frac{{{S_{2m}}}}{{{S_{2m-1}}}}$=3=a3,
若$\frac{{m}^{2}-1}{{3}^{m-1}}$=1时,即m=2时,$\frac{{{S_{2m}}}}{{{S_{2m-1}}}}$=2=a2,
所有满足条件的m值为1,2.
点评 本题考查了等比数列与等差数列的性质的判断与应用,同时考查了分类讨论的思想应用及整体思想的应用,属于中档题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AC=1,AA1=2,且P,Q,M分别是BB1,CC1,B1C1的中点,AB⊥AQ.
如图,三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AC=1,AA1=2,且P,Q,M分别是BB1,CC1,B1C1的中点,AB⊥AQ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
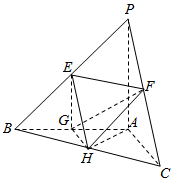 如图,在三棱锥P-ABC中,E、F、G、H分别是棱PB、PC、AB、BC的中点,PA⊥平面ABC,AB⊥AC,PA=AB=AC=2.
如图,在三棱锥P-ABC中,E、F、G、H分别是棱PB、PC、AB、BC的中点,PA⊥平面ABC,AB⊥AC,PA=AB=AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{y}^{2}}{4}$-x2=1 | C. | y2-$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | C. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.
如图所示,边长为2的正方形ABCD所在的平面与△CDE所在的平面交于CD,且AE⊥平面CDE,AE=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com