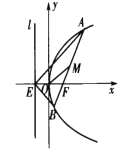
【题目】如图，已知抛物线
，
为
的焦点，
为准线，且与
轴的交点为
.过点任意作一条直线交抛物线于
两点.
（1）若
,求证：
;
（2）设
为线段
的中点，
为奇质数，且点到轴的距离和点到准线的距离均为非零整数.求证：点到坐标原点
的距离不可能是整数.
科目：高中数学 来源： 题型：
【题目】已知集合A={x|ax2+2x+1=0，a∈R}，
（1）若A只有一个元素，试求a的值，并求出这个元素；
（2）若A是空集，求a的取值范围；
（3）若A中至多有一个元素，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】据统计,某5家鲜花店今年4月的销售额和利润额资料如下表：
鲜花店名称 | A | B | C | D | E |
销售额x（千元） | 3 | 5 | 6 | 7 | 9 |
利润额y（千元） | 2 | 3 | 3 | 4 | 5 |
（1）用最小二乘法计算利润额y关于销售额x的回归直线方程
=
x+
；
（2）如果某家鲜花店的销售额为8千元时,利用(1)的结论估计这家鲜花店的利润额是多少.
参考公式：回归方程
中斜率和截距的最小二乘法估计值公式分别为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的焦距为
，椭圆
上任意一点到椭圆两个焦点的距离之和为6．
（Ⅰ）求椭圆的方程；
（Ⅱ）设直线
与椭圆交于
两点，点
（0，1），且
=
，求直线的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，直线
不与坐标轴垂直，且与抛物线
有且只有一个公共点
.
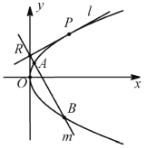
（1）当点的坐标为
时，求直线的方程；
（2）设直线与
轴的交点为
，过点且与直线垂直的直线
交抛物线
于
，
两点.当
时，求点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地环保部门跟踪调查一种有害昆虫的数量．根据调查数据，该昆虫的数量
（万只）与时间
（年）（其中
）的关系为
．为有效控制有害昆虫数量、保护生态环境，环保部门通过实时监控比值
（其中
为常数，且
）来进行生态环境分析．
（1）当
时，求比值
取最小值时
的值；
（2）经过调查，环保部门发现：当比值
不超过
时不需要进行环境防护．为确保恰好3年不需要进行保护，求实数
的取值范围．（
为自然对数的底， 
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其中常数
（1）当
时，讨论
的单调性
（2）当
时，是否存在整数
使得关于
的不等式
在区间
内有解？若存在，求出整数的最小值；若不存在，请说明理由.
参考数据：
，
，
，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一汽车厂生产
，
，
三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表(单位：辆)：按类用分层抽样的方法在这个月生产的轿车中抽取50辆，其中有类轿车10辆．
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
（1）求
的值；
（2）用分层抽样的方法在类轿车中抽取一个容量为5的样本．将该样本看成一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率；
（3）用随机抽样的方法从类舒适型轿车中抽取8辆，经检测它们的得分如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2 把这8辆轿车的得分看作一个总体，从中任取一个得分数
，记这8辆轿车的得分的平均数为
，定义事件
，且函数
没有零点
，求事件
发生的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
