
分析 依题意,知抛物线y2=-2px(p>0)的准线方程为x=$\frac{p}{2}$,设M(-9,m),利用抛物线的定义,将它到焦点的距离转化为它到其焦点的距离,从而可得答案.
解答 解:∵抛物线y2=-2px(p>0)的准线方程为x=$\frac{p}{2}$,设M(-9,m),
∵点M到焦点的距离为10,
∴由抛物线的定义知:$\frac{p}{2}$-(-9)=10,
解得:p=2,
∴抛物线方程为:y2=-4x;
将M(-9,m)点的坐标代入抛物线方程得:m2=-4×(-9)=36,
∴m=±6,
∴M点的坐标为(-9,6)或(-9,-6),
故答案为(-9,6)或(-9,-6).
点评 本题考查抛物线的标准方程,着重考查抛物线的概念,考查转化思想、分类讨论思想与运算求解能力,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:选择题
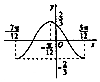 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f($\frac{π}{12}$)=( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
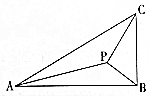 如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p | B. | ¬q | C. | p∧q | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{3}{2}$ | C. | $-\frac{8}{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com