
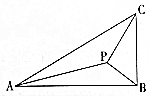
 如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$. 分析 由题意设∠PBA=α,在Rt△PBC中求出PB,在△PBA中,由∠APB=150°和内角和定理求出∠PAB,由正弦定理列出方程,由两角差的正弦函数化简后,由商的关系求出tan∠PBA的值.
解答  解:由题意知:
解:由题意知:
∠ABC=∠BPC=90°,AB=2$\sqrt{3}$,BC=2
设∠PBA=α,在Rt△PBC中,
PB=BCcos(90°-α)=2sinα,
在△PBA中,∠APB=150°,则∠PAB=30°-α,
由正弦定理得,$\frac{AB}{sin∠APB}=\frac{PB}{sin∠PAB}$,
则$\frac{2\sqrt{3}}{\frac{1}{2}}=\frac{2sinα}{sin(30°-α)}$,即$\frac{sinα}{sin(30°-α)}=2\sqrt{3}$,
sinα=2$\sqrt{3}$($\frac{1}{2}$cosα-$\frac{\sqrt{3}}{2}$sinα),
化简得4sinα=$\sqrt{3}$cosα,则tanα=$\frac{\sqrt{3}}{4}$,
所以tan∠PBA=$\frac{\sqrt{3}}{4}$,
故答案为:$\frac{\sqrt{3}}{4}$.
点评 本题考查正弦定理,两角差的正弦函数,以及商的关系的应用,考查分析问题、解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | {5} | B. | {4,5} | C. | {1,2,3} | D. | {1,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,两人分别从A村出发,其中一人沿北偏东60°方向行走了1km到了B村,另一人沿北偏西30°方向行走了$\sqrt{3}$km到了C村,问B、C两村相距多远?B村在C村的什么方向上?
如图所示,两人分别从A村出发,其中一人沿北偏东60°方向行走了1km到了B村,另一人沿北偏西30°方向行走了$\sqrt{3}$km到了C村,问B、C两村相距多远?B村在C村的什么方向上?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a<c<b | C. | c>b>a | D. | b>a>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y+3=0 | B. | 4x-2y-3=0 | C. | x+y-3=0 | D. | 2x+y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com