
| A. | x-2y+3=0 | B. | 4x-2y-3=0 | C. | x+y-3=0 | D. | 2x+y-4=0 |
分析 由已知得(s+t)($\frac{m}{s}+\frac{n}{t}$)的最小值 是$3+2\sqrt{2}$,即(s+t)($\frac{m}{s}+\frac{n}{t}$)=m+n+$\frac{mt}{s}+\frac{ns}{t}$$≥m+n+2\sqrt{mn}$,满足$\frac{mt}{s}=\frac{ns}{t}\\;即m=n$时取最小值,得m=1,n=2.设以(1,2)为中点的弦交椭圆$\frac{x^2}{4}+\frac{y^2}{16}=1$于A(x1,y1),B(x2,y2),
由中点从坐标公式知x1+x2=2,y1+y2=4,把A(x1,y1),B(x2,y2)分别代入4x2+y2=16,得$\left\{\begin{array}{l}{4{{x}_{1}}^{2}+{{y}_{1}}^{2}=16}\\{4{{x}_{2}}^{2}+{{y}_{2}}^{2}=16}\end{array}\right.$,两式相减得2(x1-x2)+(y1-y2)=0,求得k 即可
解答 解:∵sm、n、s、t为正数,m+n=3,$\frac{m}{s}+\frac{n}{t}=1$,s+t的最小值 是$3+2\sqrt{2}$,
∴(s+t)($\frac{m}{s}+\frac{n}{t}$)的最小值 是$3+2\sqrt{2}$,
∴(s+t)($\frac{m}{s}+\frac{n}{t}$)=m+n+$\frac{mt}{s}+\frac{ns}{t}$$≥m+n+2\sqrt{mn}$,满足$\frac{mt}{s}=\frac{ns}{t},\\;即m=n$时取最小值,
此时最小值为m+n+2$\sqrt{mn}$=3+2$\sqrt{2}$,得:mn=2,又:m+n=3,所以,m=1,n=2.
设以(1,2)为中点的弦交椭圆$\frac{x^2}{4}+\frac{y^2}{16}=1$于A(x1,y1),B(x2,y2),
由中点坐标公式知x1+x2=2,y1+y2=4,
把A(x1,y1),B(x2,y2)分别代入4x2+y2=16,
得$\left\{\begin{array}{l}{4{{x}_{1}}^{2}+{{y}_{1}}^{2}=16}\\{4{{x}_{2}}^{2}+{{y}_{2}}^{2}=16}\end{array}\right.$
两式相减得2(x1-x2)+(y1-y2)=0,
∴k=$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}=-2$.∴此弦所在的直线方程为y-2=-2(x-1),
即2x+y-4=0.
故选:D.
点评 本题考查了椭圆的性质和应用,解题时要认真审题,注意均值不等式和点差法的合理运用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
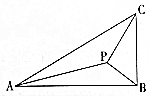 如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,两条直角边分别为AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°,若∠APB=150°,则tan∠PBA=$\frac{\sqrt{3}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p | B. | ¬q | C. | p∧q | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [9,13] | B. | (3,9) | C. | [9,+∞) | D. | (9,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\frac{1}{a}>\frac{1}{b}$,则a<b | |
| B. | 若命题$P:?x∈({0,π}),x+\frac{1}{sinx}≤2$,则?P为真命题 | |
| C. | 已知命题p,q,“p为真命题”是“p∧q为真命题”的充要条件 | |
| D. | 若f(x)为R上的偶函数,则$\int_{-1}^1{f(x)dx}=0$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com