
分析 求出命题p、p为真时m的取值范围,再根据命题p、q中有且只有一个为真命题,分p真q假和p假q真时两种情况,求出实数m的取值范围.
解答 解:命题p:椭圆C:$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{8-m}$=1的焦点在x轴上:
p为真时:m>8-m>0,解得4<m<8;
命题q:直线l:x-y+m=0与圆O:x2+y2=9有公共点;
q为真时:圆心O到直线l的距离:$d=\frac{|m|}{{\sqrt{2}}}≤3$,
解得$-3\sqrt{2}≤m≤3\sqrt{2}$;
因为命题p、q中有且只有一个为真命题,
若p真q假,则:$\left\{\begin{array}{l}4<m<8\\ m<-3\sqrt{2}或m>3\sqrt{2}\end{array}\right.$,
解得:$3\sqrt{2}<m<8$;
若p假q真,则:$\left\{\begin{array}{l}m≤4或m≥8\\-3\sqrt{2}≤m≤3\sqrt{2}\end{array}\right.$,
解得:$-3\sqrt{2}≤m≤4$;
综上,实数m的取值范围是$3\sqrt{2}<m<8$或$-3\sqrt{2}≤m≤4$.
点评 本题考查了复合命题真假的判断问题,也考查了直线与圆锥曲线的位置关系与应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{10}$ | B. | $\frac{4}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-2y+3=0 | B. | 4x-2y-3=0 | C. | x+y-3=0 | D. | 2x+y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
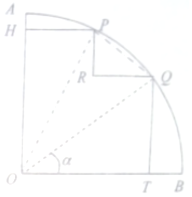 现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?
现有一圆心角为$\frac{π}{2}$,半径为12cm的扇形铁皮(如图).P,Q是弧AB上的动点且劣弧$\widehat{PQ}$的长为2πcm,过P,Q分别作与OA,OB平行或垂直的线,从扇形上裁剪出多边形OHPRQT,将该多边形面积表示为角α的函数,并求出其最大面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com