①解:f′(x)=lnmx+1,所以切线斜率为k=lnem+1=2 (1分)
所以m=1 (2分)
②解:若a>0 则当x∈[1,3],f′(x)>0,
∴f(x)单调递增,(3分)
故g(x) 在[1,3]上单调递增,从而对称轴x=a≥3,综合有a≥3 (4分)
若a<0,则当x∈[1,3],f′(x)<0,
∴f(x)单调递减,故g(x) 在[1,3]上单调递减,从而对称轴x=a≤1
综合有:a<0(6分)
若a=0,f(x) 不是单调函数,不符合题意.
综上所述:a 的取值范围是a≥3 或者a<0 (7分)
③(i)当x∈(0,

),f′(x)<0,函数单调递增,
(ii )当
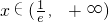
,f′(x)>0,函数单调递增
所以当

时,f(x) 取最小值
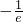
,(9分)
令
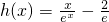
,则
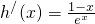
所以当x∈(0,1),h′(x)>0,h(x)单调递增,当x∈(1,+∞),h′(x)<0,h(x)单调递减
则当x=1 时,h(x) 取最大值
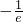
,(11分)
因此
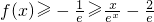
,但等号不能同时成立.
故
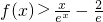
(13分)
分析:对函数求导f′(x)=lnmx+1,结合导数的几何意义可知切线斜率为k=lnem+1=2 可求m
②先求函数f(x)的单调区间,然后对a分类讨论:a>0 时,a<0,求函数y=af(x)在[1,3]上的单调性,结合二次函性质可求a的范围
③要证明x∈(0,+∞),都有
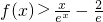
,令
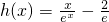
,只要证
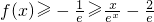
即可
点评:本题主要考查了导数的几何意义的应用,导数在判断函数的单调区间、极值、最值中的应用,及利用导数的最值与不等式证明中的应用.

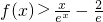 .
. ),f′(x)<0,函数单调递增,
),f′(x)<0,函数单调递增,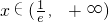 ,f′(x)>0,函数单调递增
,f′(x)>0,函数单调递增 时,f(x) 取最小值
时,f(x) 取最小值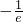 ,(9分)
,(9分)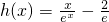 ,则
,则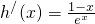
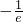 ,(11分)
,(11分)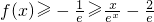 ,但等号不能同时成立.
,但等号不能同时成立.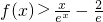 (13分)
(13分)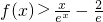 ,令
,令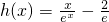 ,只要证
,只要证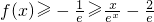 即可
即可

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<