
分析 (1)由一元二次不等式的解法可得集合A,进而由集合交集的意义计算可得答案;
(2)由一元二次不等式与一元二次方程的关系可得-3和1是方程2x2+ax+b=0的两根,进而由根与系数的关系的关系可得$\left\{\begin{array}{l}{(-3)+1=\frac{a}{2}}\\{(-3)×1=\frac{b}{2}}\end{array}\right.$,解可得a、b的值,即可得答案.
解答 解:(1)根据题意,A={x|x2-3x-4<0}={x|-1<x<4},
则A∩B={x|-1<x<1};
(2)若2x2+ax+b<0的解集为B={x|-3<x<1}.
则-3和1是方程2x2+ax+b=0的两根,
必有$\left\{\begin{array}{l}{(-3)+1=\frac{a}{2}}\\{(-3)×1=\frac{b}{2}}\end{array}\right.$,解可得a=3,b=4;
故a=4,b=-6.
点评 本题考查一元二次不等式的解法,涉及集合交集的运算,


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3条 | B. | 2条 | C. | 1条 | D. | 0条 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
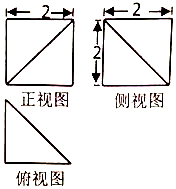
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 137 | 966 | 191 | 925 | 271 | 932 | 812 | 458 | 569 | 683 |
| 431 | 257 | 393 | 027 | 556 | 488 | 730 | 113 | 537 | 989 |
| A. | 0.40 | B. | 0.30 | C. | 0.35 | D. | 0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com