
分析 (1)求出集合A、B,根据A∩B=Φ,求出a的范围即可;
(2)分别求出p,q为真时的a的范围,取交集即可.
解答 解:(1)∵A={x|x2-3x+2≤0},B={y|y=x2-4x+a},
∴A=[1,2],B=[a-4,+∞),---------------------------4分
若p为假命题,则A∩B=Φ,故a-4>2,即a>6.-------------------------7分
(2)命题p为真,则a≤6.------------------------------8分
命题q为真,即转化为当x∈[1,2]时,f(x)=x2-ax-4≤0恒成立,--------10分
(解法1)则$\left\{\begin{array}{l}f(1)=1-a-4≤0\\ f(2)=4-2a-4≤0\end{array}$解得a≥0.--------------------------13分
{(解法2)当x∈[1,2]时,a≥x-$\frac{4}{x}$恒成立,而x-$\frac{4}{x}$在[1,2]上单调递增,故a≥(x-$\frac{4}{x}$)max=0.------------------13分 }
故实数a的取值范围是[0,6].-------------------------15分.
点评 本题考查了集合的运算性质,考查二次函数的性质以及函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
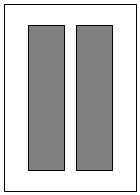 如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm
如图,要设计一张矩形广告牌,该广告牌含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,设广告牌的高为xcm,宽为ycm查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
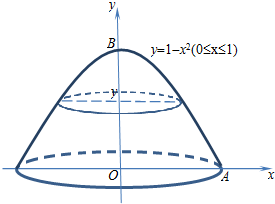 在xOy平面上,将抛物线弧y=1-x2(0≤x≤1)、x轴、y轴围成的封闭图形记为D,如图中曲边三角形OAB及内部.记D绕y轴旋转一周而成的几何体为Ω,过点(0,y)(0≤y≤1)作Ω的水平截面,所得截面面积为(1-y)π,试构造一个平放的直三棱柱,利用祖暅原理得出Ω的体积值为$\frac{π}{2}$.
在xOy平面上,将抛物线弧y=1-x2(0≤x≤1)、x轴、y轴围成的封闭图形记为D,如图中曲边三角形OAB及内部.记D绕y轴旋转一周而成的几何体为Ω,过点(0,y)(0≤y≤1)作Ω的水平截面,所得截面面积为(1-y)π,试构造一个平放的直三棱柱,利用祖暅原理得出Ω的体积值为$\frac{π}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com