Question

【题目】某健身机构统计了去年该机构所有消费者的消费金额（单位：元），如图所示：

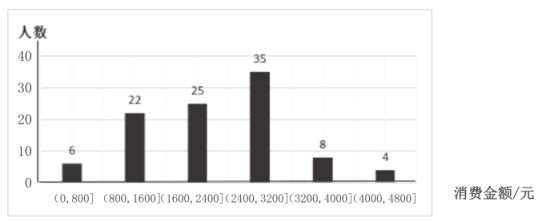
（1）现从去年的消费金额超过3200元的消费者中随机抽取2人，求至少有1位消费者，其去年的消费者金额在的范围内的概率；

（2）针对这些消费者，该健身机构今年欲实施入会制，详情如下表：

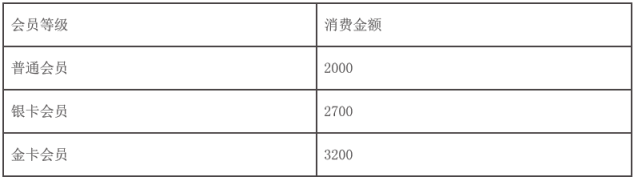
预计去年消费金额在内的消费者今年都将会申请办理普通会员，消费金额在内的消费者都将会申请办理银卡会员，消费金额在内的消费者都将会申请办理金卡会员，消费者在申请办理会员时，需一次性缴清相应等级的消费金额，该健身机构在今年底将针对这些消费者举办消费返利活动，现有如下两种预设方案：

方案1：按分层抽样从普通会员，银卡会员，金卡会员中总共抽取25位“幸运之星”给予奖励：

普通会员中的“幸运之星”每人奖励500元；银卡会员中的“幸运之星”每人奖励600元；金卡会员中的“幸运之星”每人奖励800元.

方案二：每位会员均可参加摸奖游戏，游戏规则如下：从一个装有3个白球、2个红球（球只有颜色不同）的箱子中，有放回地摸三次球，每次只能摸一个球，若摸到红球的总数为2，则可获得200元奖励金；若摸到红球的总数为3，则可获得300元奖励金；其他情况不给予奖励. 规定每位普通会员均可参加1次摸奖游戏；每位银卡会员均可参加2次摸奖游戏；每位金卡会员均可参加3次摸奖游戏（每次摸奖的结果相互独立）

请你预测哪一种返利活动方案该健身机构的投资较少？并说明理由.

Answer 1

【答案】（1）；（2）方案二.

【解析】

（1）由间接法可得到结果；（2）计算方案1奖励的总金额ξ1和方案2奖励的总金额ξ2，比较大小即可．

（1）去年的消费金额超过3200元的消费者12人，随机抽取2人，消费在的范围内的人数为X，可能取值为1，2；

P（X≥1）＝1﹣P（X＝0）＝1，

去年的消费者金额在的范围内的概率为

（2）方案1：按分层抽样从普通会员，银卡会员，金卡会员中总共抽取25位“幸运之星”，

则“幸运之星”中的普通会员，银卡会员，金卡会员的人数分别为25＝7，25＝15，25＝3，

按照方案1奖励的总金额为ξ1＝7×500+15×600+3×800＝14900（元）；

方案2：设η表示参加一次摸奖游戏所获得的奖励金，则η的可能取值为0，200，300；

由摸到红球的概率为P，

∴P（η＝0），

P（η＝200），

P（η＝300），

η的分布列为：

η	0	200	300
P

数学期望为Eη＝020030076.8（元），

按照方案2奖励的总金额为

ξ2＝（28+2×60+3×12）×76.8＝14131.2（元），

由ξ1＞ξ2知，方案2投资较少．