Question

16．执行如图所示的程序框图，若输出的结果为3，则输入的实数x的值是（　　）

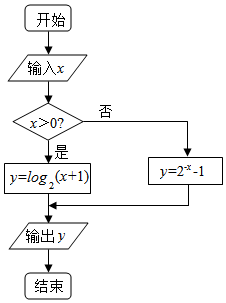
• A． -2
• B． 2
• C． 7
• D． -2或7

Answer 1

分析 根据题中程序框图的含义，得到分段函数f（x）=$\left\{\begin{array}{l}{{2}^{-x}-1，x≤0}\\{{log}_{2}（x+1），x＞0}\end{array}\right.$，
再令f（x）=3，求出x的值即可．

解答 解：根据题意，该执行该程序框图的结果是
当x≤0时，输出函数y=2^-x-1；
当x＞0时，输出函数y=log₂（x+1）；
因此，当输出结果为3时，
①若x≤0，则y=2^-x-1=3，解得x=-2；
②若x＞0，则log₂（x+1）=8，解得x=7；
综上，可输入的实数x的值是-2或7．
故选：D．

点评 本题考查了程序框图的应用问题，着重考查了对分段函数和程序框图的理解与应用问题，是基础题．