
分析 由圆的方程求出圆心坐标和半径,把过直线l:y=kx+2(k>0)上的点P作圆的切线,切线长最短转化为圆心到直线l的距离最短,由题意求得圆心到直线的距离,再代入点到直线的距离公式得答案.
解答 解:由圆(x-2)2+(y-2)2=1,
得圆的圆心坐标为(2,2),半径为1,
要使切线长最短,即圆心到直线l:y=kx+2(k>0)的距离最短,
∵圆的半径为1,切线长为$\sqrt{2}$,
∴圆心到直线l:y=kx+2(k>0)的距离等于$\sqrt{{1}^{2}+(\sqrt{2})^{2}}=\sqrt{3}$.
再由点到直线的距离公式得$\frac{|2k-2+2|}{\sqrt{{k}^{2}+1}}$=$\sqrt{3}$,解得:k=$-\sqrt{3}$(舍)或k=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查圆的切线方程,考查了直线和圆的位置关系,考查了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
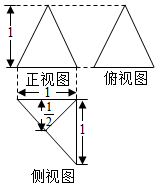 某几何体的三视图如图所示,其中正视图和侧视图是全等的等腰三角形,现从该几何体的实心外接球中挖去该几何体,则剩余几何体的体积是( )
某几何体的三视图如图所示,其中正视图和侧视图是全等的等腰三角形,现从该几何体的实心外接球中挖去该几何体,则剩余几何体的体积是( )| A. | $\frac{9π}{4}$-$\frac{1}{6}$ | B. | $\frac{9π}{16}$-$\frac{1}{2}$ | C. | $\frac{9π}{16}$-$\frac{1}{6}$ | D. | $\frac{9π}{8}$-$\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
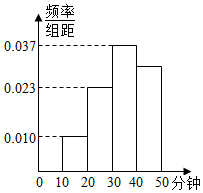 学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )
学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )| A. | 30 | B. | 40 | C. | 60 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在实施棚户区改造工程中,某居委会决定对AF地段上的危旧房进行推平改建,拟在EF地段上新建一幢居民安置楼,在EF安置楼正南面的AB地段上建一个活动中心,活动中心的侧面图由两部分构成,下部分ABCD是矩形,上部分是以CD为直径的半圆O,活动中心的规划设计需满足以下要求:①AE=30米;②AB≥AD;③当地“最斜光线”与水平线的夹角α满足tanα=$\frac{3}{4}$,活动中心在当地“最斜光线”照射下落在EF安置楼上的影长GE不超过$\frac{5}{2}$米.
如图,在实施棚户区改造工程中,某居委会决定对AF地段上的危旧房进行推平改建,拟在EF地段上新建一幢居民安置楼,在EF安置楼正南面的AB地段上建一个活动中心,活动中心的侧面图由两部分构成,下部分ABCD是矩形,上部分是以CD为直径的半圆O,活动中心的规划设计需满足以下要求:①AE=30米;②AB≥AD;③当地“最斜光线”与水平线的夹角α满足tanα=$\frac{3}{4}$,活动中心在当地“最斜光线”照射下落在EF安置楼上的影长GE不超过$\frac{5}{2}$米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com