
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
分析 设出点的坐标,求出斜率,将点的坐标代入方程,两式相减,再结合${k_{PA}}•{k_{PB}}=\frac{2}{3}$,即可求得结论.
解答 解:由mx2-ny2=1得$\frac{{x}^{2}}{\frac{1}{m}}$-$\frac{{y}^{2}}{\frac{1}{n}}$=1,
则a2=$\frac{1}{m}$,b2=$\frac{1}{n}$,则$\frac{{b}^{2}}{{a}^{2}}$=$\frac{m}{n}$
由题意,设A(x1,y1),P(x2,y2),则B(-x1,-y1)
∴kPA•kPB=$\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$,
A,B代入两式相减可得$\frac{{{y}_{2}}^{2}-{{y}_{1}}^{2}}{{{x}_{2}}^{2}-{{x}_{1}}^{2}}$=$\frac{m}{n}$,
∵${k_{PA}}•{k_{PB}}=\frac{2}{3}$,∴$\frac{m}{n}$=$\frac{2}{3}$,
∴e2=1+$\frac{{b}^{2}}{{a}^{2}}$=1+$\frac{2}{3}$=$\frac{5}{3}$,
∴e=$\frac{\sqrt{15}}{3}$.
故选:B.
点评 本题考查双曲线的标准方程,以及双曲线的简单性质的应用,利用点差法,转化为斜率之间的关系是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
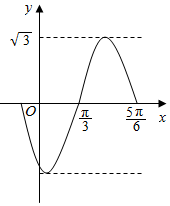 已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{2π}{3}$)(ω>0)的部分图象如图所示,则函数g(x)=cos(ωx+$\frac{2π}{3}$)的图象的一条对称轴方程为( )
已知函数f(x)=$\sqrt{3}$sin(ωx-$\frac{2π}{3}$)(ω>0)的部分图象如图所示,则函数g(x)=cos(ωx+$\frac{2π}{3}$)的图象的一条对称轴方程为( )| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{3π}{16}$ | D. | $\frac{12+3π}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com