
| A. | $\frac{2}{3}$ | B. | $-\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
分析 根据平面向量数量积的定义与投影的定义,进行计算即可.
解答 解:∵|$\overrightarrow{a}$|=2,$\overrightarrow{a}$•($\overrightarrow{b}$-$\overrightarrow{a}$)=-3,
∴$\overrightarrow{a}$•$\overrightarrow{b}$-${\overrightarrow{a}}^{2}$=$\overrightarrow{a}$•$\overrightarrow{b}$-22=-3,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=1,
∴向量$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=$\frac{1}{2}$.
故选:C.
点评 本题考查了平面向量数量积的定义与投影的计算问题,是基础题目.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
如图,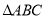 和
和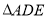 是有公共顶点的等腰直角三角形,
是有公共顶点的等腰直角三角形, ,点
,点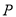 为射线
为射线 与射线
与射线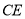 的交点.
的交点.
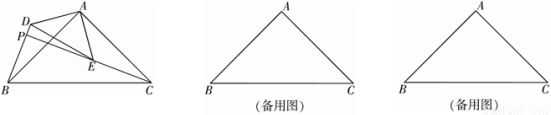
(1)求证: ;
;
(2)若 ,把
,把 绕点
绕点 旋转,
旋转,
①当 时,求
时,求 的长;
的长;
②直接写出旋转过程中线段 长的最小值与最大值.
长的最小值与最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
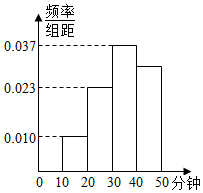 学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )
学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )| A. | 30 | B. | 40 | C. | 60 | D. | 120 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com