
分析 作出草图,根据底面△ABC与截面圆的关系计算截面半径,根据球的面积计算球的半径,利用勾股定理计算球心到截面的距离,得出棱锥P-ABC的高.
解答 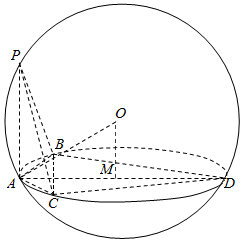 解过A作平面ABC所在球截面的直径AD,连结BD,CD,
解过A作平面ABC所在球截面的直径AD,连结BD,CD,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠ACB=∠ADC=∠ADB=30°.
∴∠BCD=∠CBD=∠BDC=60°.即△BCD是等边三角形.
∵BC=2$\sqrt{3}$,∴AD=1+3=4.
过球心O作OM⊥平面ABC,则M为AD的中点,
∴AM=2.
设外接球半径为r,则4πr2=24π,∴r=$\sqrt{6}$.即OA=$\sqrt{6}$.
∴OM=$\sqrt{2}$.
∵PA⊥平面ABC,
∴PA=2OM=2$\sqrt{2}$.
∴VP-ABC=$\frac{1}{3}×\frac{1}{2}×2\sqrt{3}×1×2\sqrt{2}$=$\frac{2\sqrt{6}}{3}$.
故答案为:$\frac{2\sqrt{6}}{3}$.
点评 本题考查棱柱、棱锥、棱台的体积,考查空间想象能力和思维能力,考查计算能力,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{3π}{16}$ | D. | $\frac{12+3π}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:解答题
某商店销售10台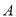 型和20台
型和20台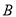 型电脑的利润为4000元,销售20台
型电脑的利润为4000元,销售20台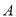 型和10台
型和10台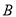 型电脑的利润为3500元.
型电脑的利润为3500元.
(1)求每台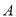 型电脑和
型电脑和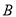 型电脑的销售利润;
型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,其中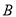 型电脑的进货量不超过A型电脑的2倍.设购进
型电脑的进货量不超过A型电脑的2倍.设购进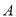 掀电脑
掀电脑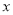 台,这100台电脑的销售总利润为
台,这100台电脑的销售总利润为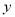 元.
元.
①求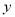 与
与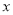 的关系式;
的关系式;
②该商店购进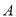 型、
型、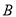 型各多少台,才能使销售利润最大?
型各多少台,才能使销售利润最大?
(3)实际进货时,厂家对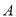 型电脑出厂价下调
型电脑出厂价下调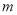 (
(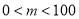 )元,且限定商店最多购进
)元,且限定商店最多购进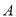 型电脑70台.若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案.
型电脑70台.若商店保持两种电脑的售价不变,请你以上信息及(2)中的条件,设计出使这100台电脑销售总利润最大的进货方案.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com