
分析 设P(x0,y0)根据定义点M与焦点F的距离等于P到准线的距离,求出x0,然后代入抛物线方程求出y0即可求出坐标.然后求解直线的斜率.
解答 解:根据定义,点P与准线的距离也是2P,
设M(x0,y0),则P与准线的距离为:x0+$\frac{p}{2}$,
∴x0+$\frac{p}{2}$=2p,x0=$\frac{3}{2}$p,
∴y0=±$\sqrt{3}$p,
∴点M的坐标($\frac{3}{2}$p,±$\sqrt{3}$p).
直线MF的斜率为:$\frac{±\sqrt{3}p}{\frac{3}{2}p}$=±$\frac{2\sqrt{3}}{3}$.
故答案为:±$\frac{2\sqrt{3}}{3}$.
点评 本题考查了抛物线的定义和性质,解题的关键是根据定义得出点M与焦点F的距离等于M到准线的距离,属于中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.
如图,在四棱锥P-ABCD中,平面PBC⊥平面ABCD,PB=PC=$\sqrt{2}$,E是PB的中点,AD∥BC,AD⊥CD,BC=2CD=2AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
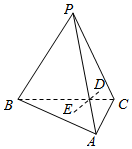 三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )
三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )| A. | DE∥PB | B. | 当AB=BC且PA=AC时DE∥PB | ||
| C. | 当且仅当AB=BC且PA=AC时,DE⊥AC | D. | DE⊥AC |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
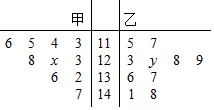 在某校统考中,甲、乙两班数学学科前10名的成绩如表:
在某校统考中,甲、乙两班数学学科前10名的成绩如表:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
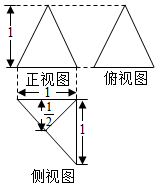 某几何体的三视图如图所示,其中正视图和侧视图是全等的等腰三角形,现从该几何体的实心外接球中挖去该几何体,则剩余几何体的体积是( )
某几何体的三视图如图所示,其中正视图和侧视图是全等的等腰三角形,现从该几何体的实心外接球中挖去该几何体,则剩余几何体的体积是( )| A. | $\frac{9π}{4}$-$\frac{1}{6}$ | B. | $\frac{9π}{16}$-$\frac{1}{2}$ | C. | $\frac{9π}{16}$-$\frac{1}{6}$ | D. | $\frac{9π}{8}$-$\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com