
| A. | -5 | B. | -$\frac{5}{9}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
分析 联立直线方程与曲线方程,求出A(0,0),B,C的横坐标为方程x2-4x+3-k=0的两根,结合|AB|=|BC|,可得方程x2-4x+3-k=0两根的关系,求出根代入即可求得k值.
解答 解:联立$\left\{\begin{array}{l}{y=kx}\\{y={x}^{3}-4{x}^{2}+3x}\end{array}\right.$,得x3-4x2+3x-kx=0,
∴x=0或x2-4x+3-k=0,
∵直线l:y=kx与曲线C:y=x3-4x2+3x顺次相交于A,B,C三点,
∴方程x2-4x+3-k=0有两不相等的实数根,
又方程x2-4x+3-k=0的对称轴方程为x=2,则方程至少有一正根,
结合对称性进一步得到方程有两正根,且A(0,0),
设B(x1,y1),C(x2,y2),
由|AB|=|BC|,得x1-0=x2-x1,即x2=2x1,
由x2-4x+3-k=0,得$x=\frac{4±\sqrt{16-4(3-k)}}{2}=2±\sqrt{k+1}$.
∴${x}_{1}=2-\sqrt{k+1},{x}_{2}=2+\sqrt{k+1}$,
则$2+\sqrt{k+1}=2(2-\sqrt{k+1})$,解得:k=-$\frac{5}{9}$.
故选:B.
点评 本题考查曲线与方程,考查了推理论证能力与运算能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\sqrt{5}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
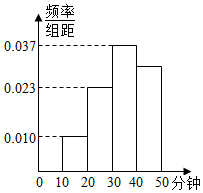 学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )
学校为了解学生每月购买学习用品方面的支出情况,抽取了n名学生进行调查,结果显示这些学生的支出(单位:元)都在[10,50]内,其频率分布直方图如图所示,其中支出在[10,30)内的学生有66人,则支出在[40,50]内的学生人数是( )| A. | 30 | B. | 40 | C. | 60 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com