下面玩掷骰子放球的游戏:若掷出1点,甲盒中放入一球;若掷出2点或是3点,乙盒中放入一球;若掷出4点或5点或6点,丙盒中放入一球!设掷n次后,甲、乙、丙盒内的球数分别为x,y,z
(1)当n=3时,求x、y、z成等差数列的概率;(2)当n=6时,求x、y、z成等比数列的概率;
(3)设掷4次后,甲盒和乙盒中球的个数差的绝对值为ξ,求Eξ.
分析:显然题目描述的是独立重复实验,但不是我们熟悉的两个而是三个,因此需要运用类比方法求解.
【答案】
分析:(1)根据x+y+z=3,且2y=x+z,求出x、y、z的值有三种情形,然后分别求出三种情形时所对应的概率,最后根据互斥事件的概率公式解之即可;
(2)根据n=6,且x、y、z成等比数列时,则x+y+z=6,且y
2=x•z求出x、y、z的值,然后根据n次独立重复试验的概率公式解之即可;
(3)ξ的可能值为0,1,2,3,4,分别根据n次独立重复试验的概率公式求出相应的概率,最后利用数学期望公式进行求解.
解答:解:(1)因x+y+z=3,且2y=x+z,所以
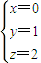
,或
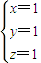
,或
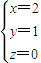
当x=0,y=1,z=2时,只投掷3次出现1次2点或3点、2次4点或5次6点,即此时的概率为

.
当x=1,y=1,z=1时,只投掷3次出现1次1点、1次2点或是3点、1次4点或5点或6点,即此时的概率为
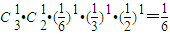
.
当x=2,y=1,z=0时,只投掷3次出现2次1点、1次2点或3点,即此时的概率为

.
故当n=3时,x,y,z成等差数列的概率为
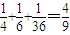
;
(2)当n=6,且x、y、z成等比数列时,由x+y+z=6,且y
2=x•z得:x=y=z=2.此时概率为
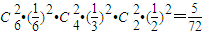
;
(3)ξ的可能值为0,1,2,3,4.
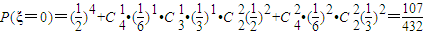

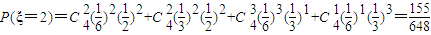
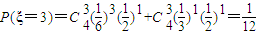
;
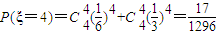
;
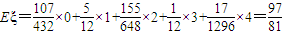
.
点评:本题主要考查了等差数列、等比数列的性质,以及离散型随机变量的期望和n次独立重复试验的概率,同时考查了计算能力,属于中档题.

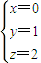 ,或
,或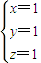 ,或
,或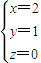
 .
.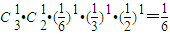 .
. .
.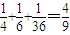 ;
;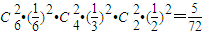 ;
;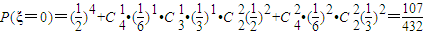

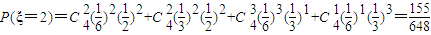
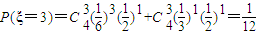 ;
;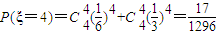 ;
;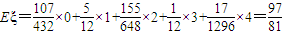 .
.

 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案