
分析 (1)先利用二倍角公式和两角差的正弦公式将函数化简为y=Asin(ωx+φ)的形式,利用周期公式求其最小正周期;
(2)根据函数图象变换规律,写出图象变换过程;
(3)先将内层函数ωx+φ看作整体,取正弦函数的五个关键点横坐标值,列出函数取值表,再依表描点,用平滑的曲线将其连接即可得函数f(x)在一个周期内的图象
解答 解:(1)f(x)=2sinx(sinx+cosx)-1,x∈R.
=2sin2x+2sinxcosx-1,
=sin2x-cos2x,
=$\sqrt{2}$sin(2x-$\frac{π}{4}$),
∴f(x)的最小正周期为T=$\frac{2π}{ω}$=π;
(2)y=sinx沿x轴向右平移$\frac{π}{4}$个单位长度得到y=sin(x-$\frac{π}{4}$),
将y=sin(x-$\frac{π}{4}$)图象横坐标缩短为原来的$\frac{1}{2}$,得到y=sin(2x-$\frac{π}{4}$),
将y=sin(2x-$\frac{π}{4}$)的图象纵坐标伸长为原来的$\sqrt{2}$倍,得到y=$\sqrt{2}$sin(2x-$\frac{π}{4}$);
(3)列表:
| 2x-$\frac{π}{4}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{5π}{8}$ | $\frac{7π}{8}$ | $\frac{9π}{8}$ |
| y | 0 | $\sqrt{2}$ | 0 | -$\sqrt{2}$ | 0 |
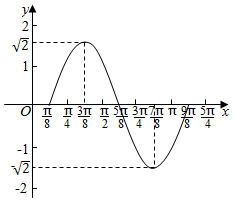
点评 本题考察了将三角函数式通过三角变换公式化为y=Asin(ωx+φ)的形式的技巧,三角恒等变换规律,三角函数的图象和性质,五点法作y=Asin(ωx+φ)型函数图象的步骤,属于中档题.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com