解:(1)
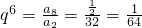
,a
n+1<a
n,
所以:

.
以

为首项.
所以,通项公式为:
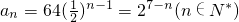
.
(2)设b
n=log
2a
n,则b
n=log
22
7-n=7-n.
所以{b
n}是首项为6,公差为-1的等差数列.
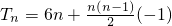
=

.
因为n是自然数,所以n=6或n=7时,T
n最大,其最值是T
6=T
7=21
分析:(1)根据等比数列的性质可知第八项与第二项的比值等于公比的六次方,利用已知即可求出公比的值,然后根据第二项的值与求出公比的值求出首项,根据首项和公比写出等比数列的通项公式即可;
(2)设b
n=log
2a
n,把第一问求出的通项公式代入即可得到b
n的通项公式,从而根据通项公式得到b
n为等差数列,根据首项和公差,根据等差数量的前n项和的公式得到T
n的通项,利用二次函数求最值的方法即可得到T
n的最大值及相应的n值.
点评:此题考查学生灵活运用等比数列的通项公式及等差数列的前n项和的公式化简求值,掌握等比数列的性质及二次函数求最值的方法,是一道综合题.

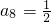 ,an+1<an.
,an+1<an.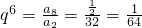 ,an+1<an,
,an+1<an, .
. 为首项.
为首项. 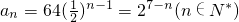 .
.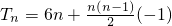 =
= .
.
