
如图,长方体ABCD﹣A1B1C1D1中,AB=3,BC=BB1=2,则异面直线AC1和B1C所成的角是( )
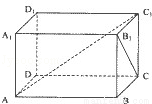
A.30° B.45° C.60° D.90°
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
(2008•崇文区二模)若半径为1的球与120°的二面角的两个半平面切于M、N两点,则两切点间的球面距离是( ).
A.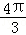 B.π C.
B.π C.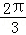 D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)>f(x)g′(x),且f(x)=ax•g(x)(a>0,且a≠1), .
. ,若数列
,若数列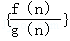 的前n项和大于62,则n的最小值为( )
的前n项和大于62,则n的最小值为( )
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
函数f1(x)=cosx﹣sinx,记f2(x)=f1′(x),f3(x)=f2′(x),…fn(x)=fn﹣1′(x),(n∈N*,n≥2),则 =( )
=( )
A.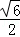 B.
B.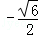 C.0 D.2008
C.0 D.2008
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.4导数的四则运算法则练习卷(解析版) 题型:?????
(2014•上海二模)已知f(x)=(2x+1)3﹣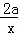 +3a,若f′(﹣1)=8,则f(﹣1)=( )
+3a,若f′(﹣1)=8,则f(﹣1)=( )
A.4 B.5 C.﹣2 D.﹣3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
若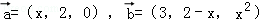 ,且
,且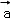 与
与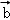 的夹角为钝角,则x的取值范围是( )
的夹角为钝角,则x的取值范围是( )
A.x<﹣4 B.﹣4<x<0 C.0<x<4 D.x>4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-1 2.5夹角的计算练习卷(解析版) 题型:?????
如图在直三棱柱ABC﹣A1B1C1中,棱AB,BC,BB1两两垂直且长度相等,点P在线段A1C1上运动,异面直线BP与B1C所成的角为θ,则θ的取值范围是( )
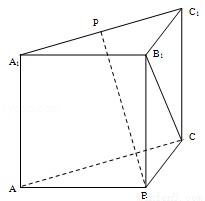
A.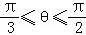 B.
B.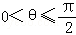 C.
C.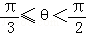 D.
D.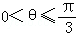
查看答案和解析>>
科目:高中数学 来源:2014-2015学年四川省成都市高三第一次诊断性检测文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列 的前
的前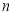 项和为
项和为 ,且
,且 ;数列
;数列 满足
满足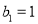 ,
,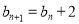 .
.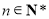 .
.
(Ⅰ)求数列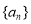 ,
, 的通项公式;
的通项公式;
(Ⅱ)记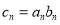 ,
,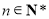 .求数列
.求数列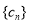 的前
的前 项和
项和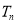 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市黄浦区高三上学期期终调研测试文科数学试卷(解析版) 题型:解答题
(本题满分14分)已知函数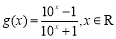 ,函数
,函数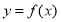 是函数
是函数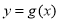 的反函数.
的反函数.
(1)求函数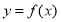 的解析式,并写出定义域
的解析式,并写出定义域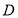 ;
;
(2) 设函数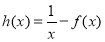 ,试判断函数
,试判断函数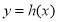 在区间
在区间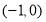 上的单调性,并说明你的理由.
上的单调性,并说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com