
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() .四边形
.四边形![]() 满足
满足![]() ,
,![]() ,
,![]() .
.![]() 为侧棱
为侧棱![]() 的中点,
的中点,![]() 为侧棱
为侧棱![]() 上的任意一点.
上的任意一点.
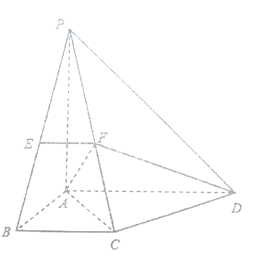
(1)若![]() 为
为![]() 的中点,求证: 面
的中点,求证: 面![]() 平面
平面![]() ;
;
(2)是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 垂直? 若存在,写出证明过程并求出线段
垂直? 若存在,写出证明过程并求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)由面面垂直的性质定理可得![]() 平面
平面![]() ,从而得
,从而得![]() ,再结合
,再结合![]() ,可得
,可得![]() 平面
平面![]() ,又利用三角形中位线定理可得
,又利用三角形中位线定理可得![]() ,进而可得结果;(2)过点
,进而可得结果;(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,先证明
,先证明![]() 平面
平面![]() ,结合
,结合![]() 平面
平面![]() ,得
,得![]() ,从而可得
,从而可得![]() 平面
平面![]() ,利用三角形面积相等即可得线段
,利用三角形面积相等即可得线段![]() 的长.
的长.
试题解析:(1)∵![]() 分别为侧棱
分别为侧棱![]() 的中点,∴
的中点,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵面![]() 平面
平面![]() ,且
,且![]() ,面
,面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,结合
,结合![]() 平面
平面![]() ,得
,得![]() .
.
又∵![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() .
.
∴ 结合![]() 平面
平面![]() ,得平面
,得平面 ![]() 平面
平面![]() .
.
(2)存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 垂直.
垂直.
平面![]() 中,过点
中,过点![]() 作
作![]() ,垂足为
,垂足为![]()
∵由己知![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴根据平面几何知识,可得![]() .
.
又∵由(1)![]() 平面
平面![]() ,得
,得 ![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() ,结合
,结合![]() 平面
平面![]() ,得
,得![]() .
.
又∵![]() ,∴
,∴![]() 平面
平面![]() .
.
在![]() 中,
中,![]() ,
, ![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∴![]() 上存在点
上存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 垂直,此时线段
垂直,此时线段![]() 长为
长为![]() .
.


科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,函数
,函数 ![]() x.
x.
(1)若g(mx2+2x+m)的定义域为R,求实数m的取值范围;
(2)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值h(a);
(3)是否存在非负实数m、n,使得函数 ![]() 的定义域为[m,n],值域为[2m,2n],若存在,求出m、n的值;若不存在,则说明理由.
的定义域为[m,n],值域为[2m,2n],若存在,求出m、n的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.在如图所示的阳马P﹣ABCD中,侧棱PD⊥底面ABCD,且PD=CD,点E是PC的中点,连接DE,BD,BE. 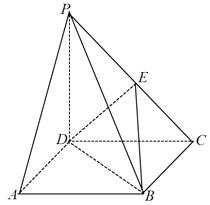
(1)证明:DE⊥平面PBC.
(2)试判断四面体EBCD是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,请说明理由;
(3)记阳马P﹣ABCD的体积为V1 , 四面体EBCD的体积为V2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. 将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后得到函数
个单位后得到函数![]() 的图象
的图象
B. 函数![]() 图象关于点
图象关于点![]() 中心对称
中心对称
C. 函数![]() 的图象关于
的图象关于![]() 对称
对称
D. 函数![]() 在区间
在区间![]() 内单调递增
内单调递增
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(1,2),B(﹣1,2),动点P满足 ![]() ,若双曲线
,若双曲线 ![]() =1(a>0,b>0)的渐近线与动点P的轨迹没有公共点,则双曲线离心率的取值范围是 .
=1(a>0,b>0)的渐近线与动点P的轨迹没有公共点,则双曲线离心率的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(﹣∞,0)∪(0,+∞),f(x)是奇函数,且当x>0时,f(x)=x2﹣x+a,若函数g(x)=f(x)﹣x的零点恰有两个,则实数a的取值范围是( )
A.a<0
B.a≤0
C.a≤1
D.a≤0或a=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com