
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源:2017届福建福州外国语学校高三文上学期期中数学试卷(解析版) 题型:选择题
定义在 上的函数
上的函数 满足
满足 ,
, 为
为 的导函数,已知函数
的导函数,已知函数 的图象如图所示,若两正数
的图象如图所示,若两正数 满足
满足 ,则
,则 的取值范围是( )
的取值范围是( )

A.( ,
, ) B.(-∞,
) B.(-∞, )∪(3,+∞)
)∪(3,+∞)
C.( ,3) D.(-∞,-3)
,3) D.(-∞,-3)
查看答案和解析>>
科目:高中数学 来源:2017届甘肃肃南裕固族自治县一中高三理12月月考数学试卷(解析版) 题型:解答题
已知函数 在
在 处取得最值,其中
处取得最值,其中 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)将函数 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标伸长为原来的3倍,纵坐标不变,得到函数
个单位,再将所得图象上各点的横坐标伸长为原来的3倍,纵坐标不变,得到函数 的图象,若
的图象,若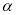 为锐角,
为锐角, ,求
,求 .
.
查看答案和解析>>
科目:高中数学 来源:2017届甘肃肃南裕固族自治县一中高三理12月月考数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输出的 ,则输入的整数
,则输入的整数 的最大值是( )
的最大值是( )

A.18 B.50
C. 78 D.306
查看答案和解析>>
科目:高中数学 来源:2017届甘肃肃南裕固族自治县一中高三文12月月考数学试卷(解析版) 题型:解答题
已知椭圆 的离心率
的离心率 ,过椭圆的左焦点
,过椭圆的左焦点 且倾斜角为30°的直线与圆
且倾斜角为30°的直线与圆 相交所得弦的长度为1.
相交所得弦的长度为1.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若动直线 交椭圆
交椭圆 于不同两点
于不同两点 ,设
,设 ,
, 为坐标原点.当以线段
为坐标原点.当以线段 为直径的圆恰好过点
为直径的圆恰好过点 时,求证:
时,求证: 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源:2017届广东汕头市高三理上学期期末数学试卷(解析版) 题型:解答题
为评估设备 生产某种零件的性能,从设备
生产某种零件的性能,从设备 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值 ,标准差
,标准差 ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(Ⅰ)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为 ,并根据以下不等式进行评判(
,并根据以下不等式进行评判( 表示相应事件的概率);①
表示相应事件的概率);①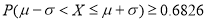 ;
;
② ;③
;③ .
.
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备 的性能等级.
的性能等级.
(2)将直径小于等于 或直径大于
或直径大于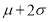 的零件认为是次品.
的零件认为是次品.
(ⅰ)从设备 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数 的数学期望
的数学期望 ;
;
(ⅱ)从样本中随意抽取2件零件,计算其中次品个数 的数学期望
的数学期望 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com