
分析 (1)求出不等式|x-2|>3的解集,即得不等式x2-ax+b>0的解集,利用一元二次方程根与系数的关系求出 a和b的值,
(2)根据柯西不等式即可求出最大值.
解答 解:(1)不等式|x-2|>3的解集为{x|x<-1或x>5},所以不等式x2-ax-b>0的解集为{x|x<-1或x>5},
所以-1,5是方程x2-ax-b=0的两根,所以$\left\{\begin{array}{l}{1+a-b=0}\\{25-5a-b=0}\end{array}\right.$,解得a=4,b=5.
(2)函数f(x)=a$\sqrt{x-3}$+b$\sqrt{44-x}$的定义域为[3,44],由柯西不等式得:
[f(x)]2=(4$\sqrt{x-3}$+5$\sqrt{44-x}$)2≤[(16+25)(x-3+44-x)]2,.
又因为f(x)≥0,所以f(x)≤4,当且仅当5$\sqrt{x-3}$=4$\sqrt{44-x}$时等号成立,
即x=$\frac{779}{41}$时,f(x)=41.所以函数f(x)的最大值为41.
点评 本题主要考查绝对值不等式的解法,一元二次方程根与系数的关系,以及柯西不等式,考查转化能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 4500 | B. | 4505 | C. | 4514 | D. | 4519 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 求1×2×3×4×…×10000的值 | |
| B. | 求2×4×6×8×…×10000的值 | |
| C. | 求3×5×7×9×…×10001的值 | |
| D. | 求满足1×3×5×…×n>10000的最小正整数n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
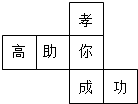 水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )| A. | 左面,后面,上面 | B. | 后面,上面,左面 | C. | 上面,左面,后面 | D. | 后面,左面,上面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com