
【题目】已知函数![]() (
(![]() )的图象上的动点
)的图象上的动点![]() 到原点
到原点![]() 的距离的平方的最小值为
的距离的平方的最小值为![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() ,若函数
,若函数![]() 有两个极值点
有两个极值点![]() 、
、![]() ,且
,且![]() ,证明:
,证明:![]() .(参考公式:
.(参考公式:![]() )
)
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为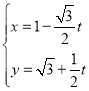 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,以x轴正半轴为极轴,建立极坐标系,曲线
为极点,以x轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 、
、![]() 为曲线
为曲线![]() 上位于第一,二象限的两个动点,且
上位于第一,二象限的两个动点,且![]() ,射线
,射线![]() ,
,![]() 交曲线
交曲线![]() 分别于点
分别于点![]() ,
,![]() .求
.求![]() 面积的最小值,并求此时四边形
面积的最小值,并求此时四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂制作如图所示的一种标识,在半径为R的圆内做一个关于圆心对称的“H型”图形,“H”型图形由两竖一横三个等宽的矩形组成,两个竖直的矩形全等且它们的长边是横向矩形长边的![]() 倍,设O为圆心,
倍,设O为圆心,![]() ,“H”型图形的面积为S.
,“H”型图形的面积为S.
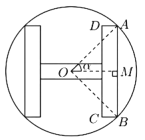
(1)将AB、AD用R、![]() 表示,并将S表示成
表示,并将S表示成![]() 的函数;
的函数;
(2)为了突出“H”型图形,设计时应使S尽可能大,则当![]() 为何值时,S最大?并求出S的最大值.
为何值时,S最大?并求出S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线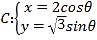 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() ,点
,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的参数方程;
的参数方程;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com