
【题目】如图,直三棱柱![]() 的底面为等边三角形,
的底面为等边三角形,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)推导出![]() 平面
平面![]() ,可得出
,可得出![]() ,结合
,结合![]() ,利用线面垂直的判定定理可得出
,利用线面垂直的判定定理可得出![]() 平面
平面![]() ,再由面面垂直的判定定理可证得结论成立;
,再由面面垂直的判定定理可证得结论成立;
(2)由![]() 平面
平面![]() 得出
得出![]() ,利用勾股定理计算出
,利用勾股定理计算出![]() 的长,然后以点
的长,然后以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,利用空间向量法可求出二面角
,利用空间向量法可求出二面角![]() 的余弦值.
的余弦值.
(1)因为三棱柱![]() 为直三棱柱,所以
为直三棱柱,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
因为![]() 为等边三角形,
为等边三角形,![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)由(1)可知![]() 平面
平面![]() ,所以
,所以![]() .
.
设![]() ,则有
,则有![]() ,即
,即![]() ,得
,得![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
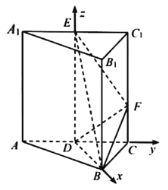
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() ,
,
由 ,令
,令![]() ,可得
,可得![]() ,
,![]() ,则
,则![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
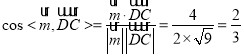 ,
,
由图形可知,二面角![]() 的平面角为锐角,所以二面角
的平面角为锐角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数,各项均为正整数的数列
为正整数,各项均为正整数的数列![]() 满足:
满足: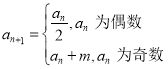 ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 为奇数,求证:“
为奇数,求证:“![]() ”的充要条件是“
”的充要条件是“![]() 为奇数”.
为奇数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为提升中学生的数学素养,激发学生学习数学的兴趣,举办了一次“数学文化知识大赛”,分预赛和复赛两个环节.已知共有8000名学生参加了预赛,现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本,得到如下频率分布直方图.

(1)规定预赛成绩不低于80分为优良,若从上述样本中预赛成绩不低于60分的学生中随机地抽取2人,求恰有1人预赛成绩优良的概率;
(2)由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布N(μ,σ2),其中μ可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且σ2=362.利用该正态分布,估计全市参加预赛的全体学生中预赛成绩不低于91分的人数;
(3)预赛成绩不低于91分的学生将参加复赛,复赛规则如下:①每人的复赛初始分均为100分;②参赛学生可在开始答题前自行决定答题数量n,每一题都需要“花”掉(即减去)一定分数来获取答题资格,规定答第k题时“花”掉的分数为0.1k(k∈(1,2n));③每答对一题加1.5分,答错既不加分也不减分;④答完n题后参赛学生的最终分数即为复赛成绩.已知学生甲答对每道题的概率均为0.7,且每题答对与否都相互独立.若学生甲期望获得最佳的复赛成绩,则他的答题数量n应为多少?
(参考数据:![]() ;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为D,若存在实常数
的定义域为D,若存在实常数![]() 及
及![]() ,对任意
,对任意![]() ,当
,当![]() 且
且![]() 时,都有
时,都有![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断函数![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)若函数![]() 具有性质
具有性质![]() ,求
,求![]() 及
及![]() 应满足的条件;
应满足的条件;
(3)已知函数![]() 不存在零点,当
不存在零点,当![]() 时具有性质
时具有性质![]() (其中
(其中![]() ,
,![]() ),记
),记![]() ,求证:数列
,求证:数列![]() 为等比数列的充要条件是
为等比数列的充要条件是![]() 或
或![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com