
【题目】已知![]() 为正整数,各项均为正整数的数列
为正整数,各项均为正整数的数列![]() 满足:
满足: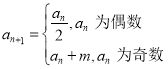 ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 为奇数,求证:“
为奇数,求证:“![]() ”的充要条件是“
”的充要条件是“![]() 为奇数”.
为奇数”.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)利用递推公式直接代入求值.
(2)分类讨论当![]() 为奇数和偶数的情况,再讨论
为奇数和偶数的情况,再讨论![]() 为奇数和偶数的情况,求得
为奇数和偶数的情况,求得![]() 的值.
的值.
(3)先证充分性(易证得),再证必要性,用数学归纳法证明.
解:(1)![]() ,
,![]() ,则前7项为8,4,2,1,3,5,7,故
,则前7项为8,4,2,1,3,5,7,故![]() .
.
(2)由题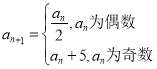 设
设![]() 是整数.
是整数.
①若![]() 为奇数,可设
为奇数,可设![]() ,
,![]() ,则
,则![]() 是偶数,得
是偶数,得![]() ,
,
则![]() ,此时
,此时![]() ,符合题意
,符合题意
②若![]() 为偶数,可设
为偶数,可设![]() ,
,![]() ,则
,则![]() ,
,
当![]() 是偶数时,可设
是偶数时,可设![]() ,得
,得![]()
![]() ,
,![]() ,
,
则![]() ,此时
,此时![]() 不存在.
不存在.
当![]() 是奇数时,可设
是奇数时,可设![]() ,得
,得![]() ,
,![]() ,
,
![]() ,则
,则![]() ,得
,得![]() ,得
,得![]() .
.
综合①②可得,![]() 或
或![]() .
.
(3)充分性:若![]() 为奇数,则
为奇数,则![]() ;
;
必要性:先利用数学归纳法证:![]() (
(![]() 为奇数);
为奇数);![]() (
(![]() 为偶数).
为偶数).
①![]() ,
,![]() ,
,![]() 成立;
成立;
②假设![]() 时,
时,![]() (
(![]() 为奇数);
为奇数);![]() (
(![]() 为偶数).
为偶数).
③当![]() 时,当
时,当![]() 是偶数,
是偶数,![]() ;当
;当![]() 是奇数,
是奇数,![]() ,此时
,此时![]() 是偶数.
是偶数.
综上,由数学归纳法得![]() (
(![]() 为奇数);
为奇数);![]() (
(![]() 为偶数).
为偶数).
从而若![]() 时,必有
时,必有![]() 是偶数.进而若
是偶数.进而若![]() 是偶数,则
是偶数,则![]() 矛盾,故
矛盾,故![]() 只能为奇数.
只能为奇数.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】某学校开设了射击选修课,规定向![]() 、
、![]() 两个靶进行射击:先向
两个靶进行射击:先向![]() 靶射击一次,命中得1分,没有命中得0分,向
靶射击一次,命中得1分,没有命中得0分,向![]() 靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向
靶连续射击两次,每命中一次得2分,没命中得0分;小明同学经训练可知:向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,向
,向![]() 靶射击,命中的概率为
靶射击,命中的概率为![]() ,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
,假设小明同学每次射击的结果相互独立.现对小明同学进行以上三次射击的考核.
(1)求小明同学恰好命中一次的概率;
(2)求小明同学获得总分![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 中,
中,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上.数列
上.数列![]() 中,点
中,点![]() 在经过点
在经过点![]() ,以
,以![]() 为方向向量的直线
为方向向量的直线![]() 上.
上.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若 ,问是否存在
,问是否存在![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)对任意的正整数![]() ,不等式
,不等式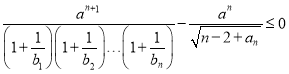 成立,求正数
成立,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长为5的菱形ABCD沿对角线AC折起,顶点B移动至![]() 处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
A.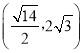 B.
B. C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校艺术学院2019级表演专业有27人,播音主持专业9人,影视编导专业18人.某电视台综艺节目招募观众志愿者,现采用分层抽样的方法从上述三个专业的人员中选取6人作为志愿者.
(1)分别写出各专业选出的志愿者人数;
(2)将6名志愿者平均分成三组,且每组的两名同学选自不同的专业,通过适当的方式列出所有可能的结果,并求表演专业的志愿者![]() 与播音主持专业的志愿者分在一组的概率.
与播音主持专业的志愿者分在一组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com