
【题目】将边长为5的菱形ABCD沿对角线AC折起,顶点B移动至![]() 处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
处,在以点B',A,C,为顶点的四面体AB'CD中,棱AC、B'D的中点分别为E、F,若AC=6,且四面体AB'CD的外接球球心落在四面体内部,则线段EF长度的取值范围为( )
A.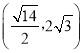 B.
B. C.
C.![]() D.
D.![]()
【答案】B
【解析】
由题意画出图形,可证AC⊥平面B′ED,得到球心O位于平面B′ED与平面ACF的交线上,即直线EF上,由勾股定理结合OA=OB′,OE<EF,EF<EB′=4可得线段EF长度的取值范围.
如图所示:

由已知可得,AC⊥B′E,且AC⊥DE,
∴AC⊥平面B′ED,
∵E是AC的中点,
∴到点A、C的距离相等的点位于平面ACF内,
同理可知,到点B′、D的距离相等的点位于平面ACF内,
∵球心O到点A,B′,C,D的距离相等,
∴球心O位于平面B′ED与平面ACF的交线上,即直线EF上.
∴球心O落在线段EF上(不含端点E、F),
显然EF⊥B′D,由题意EA=3,EB′=4,则OA2=OE2+9,
且OB′2=OF2+FB′2=OF2+EB′2﹣EF2=(EF﹣OE)2+16﹣EF2=OE2+16﹣2EFOE.
∵OA=OB′,
∴OE2+9=OE2+16﹣2EFOE,则![]() ,
,
显然OE<EF,
∴![]() EF,即EF
EF,即EF![]() .
.
又EF<EB′=4,∴![]() EF<4.
EF<4.
故选:B.


科目:高中数学 来源: 题型:
【题目】已知项数为![]() 的数列
的数列![]() 满足条件:①
满足条件:①![]() ;②
;②![]() ;若数列
;若数列![]() 满足
满足![]() ,则称
,则称![]() 为数列
为数列![]() 的“关联数列.
的“关联数列.
(1)数列1,5,9,13,17是否存在“关联数列”?若存在,写出其“关联数列”,若不存在,请说明理由;
(2)若数列![]() 存在“关联数列”
存在“关联数列”![]() ,证明:
,证明:![]() ;
;
(3)已知数列![]() 存在“关联数列”
存在“关联数列”![]() ,且
,且![]() ,
,![]() ,求数列
,求数列![]() 项数m的最小值与最大值.
项数m的最小值与最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
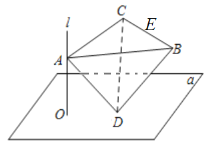
【题目】如图,直线![]() 平面
平面![]() ,垂足为
,垂足为![]() ,正四面体
,正四面体![]() 的棱长为2,
的棱长为2,![]() ,
,![]() 分别是直线
分别是直线![]() 和平面
和平面![]() 上的动点,且
上的动点,且![]() ,则下列判断:①点
,则下列判断:①点![]() 到棱
到棱![]() 中点
中点![]() 的距离的最大值为
的距离的最大值为![]() ;②正四面体
;②正四面体![]() 在平面
在平面![]() 上的射影面积的最大值为
上的射影面积的最大值为![]() .其中正确的说法是( ).
.其中正确的说法是( ).
A.①②都正确B.①②都错误C.①正确,②错误D.①错误,②正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数,各项均为正整数的数列
为正整数,各项均为正整数的数列![]() 满足:
满足: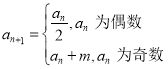 ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 为奇数,求证:“
为奇数,求证:“![]() ”的充要条件是“
”的充要条件是“![]() 为奇数”.
为奇数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
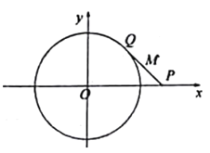
【题目】已知![]() 是
是![]() 轴上的动点(异于原点
轴上的动点(异于原点![]() ),点
),点![]() 在圆
在圆![]() 上,且
上,且![]() .设线段
.设线段![]() 的中点为
的中点为![]() ,当点
,当点![]() 移动时,记点
移动时,记点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)当直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且点
,且点![]() 在第一象限.
在第一象限.
(ⅰ)求直线![]() 的斜率;
的斜率;
(ⅱ)直线![]() 平行
平行![]() ,交曲线
,交曲线![]() 于不同的两点
于不同的两点![]() 、
、![]() .线段
.线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() 、
、![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为提升中学生的数学素养,激发学生学习数学的兴趣,举办了一次“数学文化知识大赛”,分预赛和复赛两个环节.已知共有8000名学生参加了预赛,现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本,得到如下频率分布直方图.

(1)规定预赛成绩不低于80分为优良,若从上述样本中预赛成绩不低于60分的学生中随机地抽取2人,求恰有1人预赛成绩优良的概率;
(2)由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布N(μ,σ2),其中μ可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且σ2=362.利用该正态分布,估计全市参加预赛的全体学生中预赛成绩不低于91分的人数;
(3)预赛成绩不低于91分的学生将参加复赛,复赛规则如下:①每人的复赛初始分均为100分;②参赛学生可在开始答题前自行决定答题数量n,每一题都需要“花”掉(即减去)一定分数来获取答题资格,规定答第k题时“花”掉的分数为0.1k(k∈(1,2n));③每答对一题加1.5分,答错既不加分也不减分;④答完n题后参赛学生的最终分数即为复赛成绩.已知学生甲答对每道题的概率均为0.7,且每题答对与否都相互独立.若学生甲期望获得最佳的复赛成绩,则他的答题数量n应为多少?
(参考数据:![]() ;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为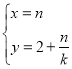 (
(![]() 为参数).设直线
为参数).设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时的点
变化时的点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,设射线
轴正半轴为极轴建立极坐标系,设射线![]() 的极坐标方程为
的极坐标方程为![]() 且
且![]() ,点
,点![]() 是射线
是射线![]() 与曲线
与曲线![]() 的交点,求点
的交点,求点![]() 的极径.
的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面α∩平面β=l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )
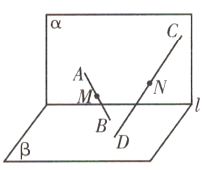
A.若AB![]() CD,则MN
CD,则MN![]() l
l
B.若M,N重合,则AC![]() l
l
C.若AB与CD相交,且AC![]() l,则BD可以与l相交
l,则BD可以与l相交
D.若AB与CD是异面直线,则MN不可能与l平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 为等边三角形,且垂直于底面
为等边三角形,且垂直于底面![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)已知点![]() 在棱
在棱![]() 上且
上且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com