
【题目】若实数![]() ,
,![]() 满足
满足 则
则![]() 的取值范围为________.
的取值范围为________.
【答案】![]()
【解析】
分4种情况进行讨论,对于每种情况,作出相应的可行域,再作出目标函数对应的直线,平移该直线,即可求出每种情况中![]() 的取值范围,从而得解.
的取值范围,从而得解.
设目标函数![]() ,
,
分四种情况:
(1)当 时,
时,![]() ,
,
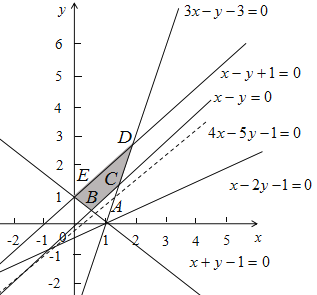
画出满足条件的平面区域,如图所示,

满足约束条件的平面区域,只有一个点![]() ,此时
,此时![]() ;
;
(2)当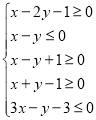 时,
时,![]() ,
,
满足约束条件的平面区域不存在;
(3)当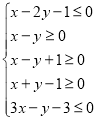 时,
时,![]() ,
,
画出满足条件的平面区域,如图所示,
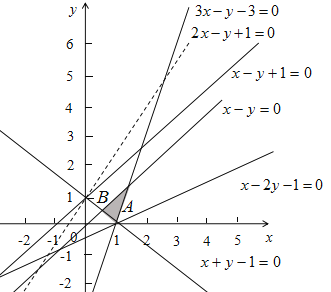
![]() ,得
,得![]() ,
,
显然直线过![]() 与
与![]() 的交点
的交点![]() 时,
时,![]() 最小,
最小,
![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
直线过![]() 与
与![]() 的交点
的交点![]() 时,
时,![]() 最大,
最大,
![]() ,解得
,解得![]() ,此时
,此时![]() ;
;
(4)当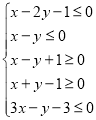 时,
时,![]() ,
,
画出满足条件的平面区域,如图所示,
![]() ,得
,得![]() ,
,
显然直线过![]() 与
与![]() 的交点
的交点![]() 时,
时,![]() 最小,
最小,
![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
直线过![]() 与
与![]() 的交点
的交点![]() 时,
时,![]() 最大,
最大,
![]() ,解得
,解得![]() ,此时
,此时![]() .
.
综上可知,![]() 的最小值为
的最小值为![]() ,最大值为8,
,最大值为8,
即![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.出现的新型冠状病毒(nCoV)是从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检测血液中的指标![]() .现从采集的血液样品中抽取500份检测指标
.现从采集的血液样品中抽取500份检测指标![]() 的值,由测量结果得下侧频率分布直方图:
的值,由测量结果得下侧频率分布直方图:

(1)求这500份血液样品指标![]() 值的平均数
值的平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表,记作
(同一组数据用该区间的中点值作代表,记作![]() );
);
(2)由频率分布直方图可以认为,这项指标![]() 的值X服从正态分布
的值X服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .在统计学中,把发生概率小于3‰的事件称为小概率事件(正常条件下小概率事件的发生是不正常的).该医院非常关注本院医生健康状况,随机抽取20名医生,独立的检测血液中指标
.在统计学中,把发生概率小于3‰的事件称为小概率事件(正常条件下小概率事件的发生是不正常的).该医院非常关注本院医生健康状况,随机抽取20名医生,独立的检测血液中指标![]() 的值,结果发现4名医生血液中指标
的值,结果发现4名医生血液中指标![]() 的值大于正常值20.03,试根据题中条件判断该院医生的健康率是否正常,并说明理由.
的值大于正常值20.03,试根据题中条件判断该院医生的健康率是否正常,并说明理由.
附:参考数据与公式:![]() ,
,![]() ,
,![]() ;若
;若![]() ,则①
,则①![]() ;②
;②![]() ;③
;③![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列的极限一节,课本中给出了计算由抛物线![]() 、
、![]() 轴以及直线
轴以及直线![]() 所围成的曲边区域面积
所围成的曲边区域面积![]() 的一种方法:把区间
的一种方法:把区间![]() 平均分成
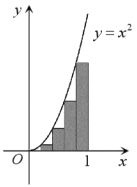
平均分成![]() 份,在每一个小区间上作一个小矩形,使得每个矩形的左上端点都在抛物线
份,在每一个小区间上作一个小矩形,使得每个矩形的左上端点都在抛物线![]() 上(如图),则当
上(如图),则当![]() 时,这些小矩形面积之和的极限就是
时,这些小矩形面积之和的极限就是![]() .已知
.已知![]() .利用此方法计算出的由曲线
.利用此方法计算出的由曲线![]() 、
、![]() 轴以及直线
轴以及直线![]() 所围成的曲边区域的面积为( )
所围成的曲边区域的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行调查,通过抽样,获得某年100为居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
(1)求直方图的![]() 的值;
的值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由.
(3)估计居民月用水量的中位数.

查看答案和解析>>
科目:高中数学 来源: 题型:
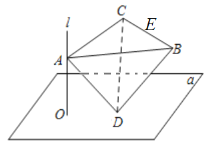
【题目】如图,直线![]() 平面
平面![]() ,垂足为
,垂足为![]() ,正四面体
,正四面体![]() 的棱长为2,
的棱长为2,![]() ,
,![]() 分别是直线
分别是直线![]() 和平面
和平面![]() 上的动点,且
上的动点,且![]() ,则下列判断:①点
,则下列判断:①点![]() 到棱
到棱![]() 中点
中点![]() 的距离的最大值为
的距离的最大值为![]() ;②正四面体
;②正四面体![]() 在平面
在平面![]() 上的射影面积的最大值为
上的射影面积的最大值为![]() .其中正确的说法是( ).
.其中正确的说法是( ).
A.①②都正确B.①②都错误C.①正确,②错误D.①错误,②正确
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数,各项均为正整数的数列
为正整数,各项均为正整数的数列![]() 满足:
满足: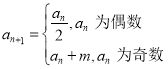 ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 为奇数,求证:“
为奇数,求证:“![]() ”的充要条件是“
”的充要条件是“![]() 为奇数”.
为奇数”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为提升中学生的数学素养,激发学生学习数学的兴趣,举办了一次“数学文化知识大赛”,分预赛和复赛两个环节.已知共有8000名学生参加了预赛,现从参加预赛的全体学生中随机地抽取100人的预赛成绩作为样本,得到如下频率分布直方图.

(1)规定预赛成绩不低于80分为优良,若从上述样本中预赛成绩不低于60分的学生中随机地抽取2人,求恰有1人预赛成绩优良的概率;
(2)由频率分布直方图可认为该市全体参加预赛学生的预赛成绩Z服从正态分布N(μ,σ2),其中μ可近似为样本中的100名学生预赛成绩的平均值(同一组数据用该组区间的中点值代替),且σ2=362.利用该正态分布,估计全市参加预赛的全体学生中预赛成绩不低于91分的人数;
(3)预赛成绩不低于91分的学生将参加复赛,复赛规则如下:①每人的复赛初始分均为100分;②参赛学生可在开始答题前自行决定答题数量n,每一题都需要“花”掉(即减去)一定分数来获取答题资格,规定答第k题时“花”掉的分数为0.1k(k∈(1,2n));③每答对一题加1.5分,答错既不加分也不减分;④答完n题后参赛学生的最终分数即为复赛成绩.已知学生甲答对每道题的概率均为0.7,且每题答对与否都相互独立.若学生甲期望获得最佳的复赛成绩,则他的答题数量n应为多少?
(参考数据:![]() ;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
;若Z~N(μ,σ2),则P(μ﹣σ<Z<μ+σ)≈0.6827,P(μ﹣2σ<Z<μ+2σ)≈0.9545,P(μ﹣3σ<Z<μ+3σ)≈0.9973.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2a=2bcosC+csinB.
(Ⅰ)求tanB;
(Ⅱ)若C![]() ,△ABC的面积为6,求BC.
,△ABC的面积为6,求BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com