
【题目】已知函数![]() ,且存在
,且存在![]() ,使得
,使得![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明![]() 单调递增;
单调递增;
(Ⅱ)求证:![]() ;
;
(Ⅲ)记![]() ,其前
,其前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ)证明见解析
【解析】
(Ⅰ)首先求出![]() ,然后通过证明
,然后通过证明![]() 恒成立即可;
恒成立即可;
(Ⅱ)利用数学归纳法,即首先验证![]() 时不等式是否成立,然后假设当
时不等式是否成立,然后假设当![]() 时不等式成立,再通过验证
时不等式成立,再通过验证![]() 时不等式是否成立使问题得证;
时不等式是否成立使问题得证;
(Ⅲ)利用(Ⅱ)的结论,先放缩再结合等比数列的求和公式即可证明.
(Ⅰ)由函数![]() ,则
,则![]() ,
,
所以![]() 是
是![]() 上的单调递增函数.
上的单调递增函数.
(Ⅱ)因为![]() ,即
,即![]() .
.
又因为![]() 是单调递增函数,可得
是单调递增函数,可得![]() ,即
,即![]() .
.
又由![]() ,
,![]() ,
,
综上可得![]() .
.
用数学归纳法证明如下:
①当![]() 时,上面已证明成立.
时,上面已证明成立.
②假设当![]() 时,有
时,有![]() ,
,
则当![]() 时,由
时,由![]() 是单调递增函数,可得
是单调递增函数,可得![]() ,
,
所以![]() ,
,
由①②知对一切![]() 都有
都有![]() .
.
(Ⅲ)因为![]()
![]()
![]() .
.
由(Ⅱ)知![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以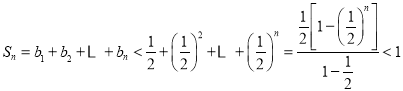 .
.
综上可得![]() .
.


科目:高中数学 来源: 题型:
【题目】阿波罗尼斯(约公元前![]() 年)证明过这样一个命题:平面内到两定点距离之比为常数
年)证明过这样一个命题:平面内到两定点距离之比为常数![]() 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点![]() 、
、![]() 间的距离为
间的距离为![]() ,动点
,动点![]() 满足
满足![]() ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村共有100户农民,且都从事蔬菜种植,平均每户的年收入为2万元.为了调整产业结构,该镇政府决定动员部分农民从事蔬菜加工.据估计,若能动员![]() 户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高
户农民从事蔬菜加工,则剩下的继续从事蔬菜种植的农民平均每户的年收入比上一年提高![]() ,而从事蔬菜加工的农民平均每户的年收入为
,而从事蔬菜加工的农民平均每户的年收入为![]() 万元.
万元.
(1)在动员![]() 户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求
户农民从事蔬菜加工后,要使从事蔬菜种植的农民的总年收入不低于动员前100户农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事蔬菜加工的农民的总年收入始终不高于从事蔬菜种植的农民的总年收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的
年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的![]() 次线上测试成绩进行统计如图所示:
次线上测试成绩进行统计如图所示:
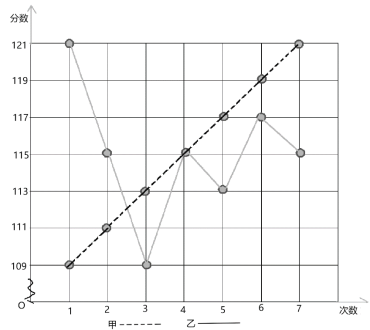
(1)请填写下表(要求写出计算过程)
平均数 | 方差 | |
甲 | ||
乙 |
(2)从下列三个不同的角度对这次方案选择的结果进行
①从平均数和方差相结合看(分析哪种方案的成绩更好);
②从折线图上两种方案的走势看(分析哪种方案更有潜力).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为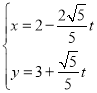 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)设点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且
上的点,且![]() .求
.求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com