
【题目】已知函数![]() 的定义域为D,若存在实常数
的定义域为D,若存在实常数![]() 及
及![]() ,对任意
,对任意![]() ,当
,当![]() 且
且![]() 时,都有
时,都有![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断函数![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)若函数![]() 具有性质
具有性质![]() ,求
,求![]() 及
及![]() 应满足的条件;
应满足的条件;
(3)已知函数![]() 不存在零点,当
不存在零点,当![]() 时具有性质
时具有性质![]() (其中
(其中![]() ,
,![]() ),记
),记![]() ,求证:数列
,求证:数列![]() 为等比数列的充要条件是
为等比数列的充要条件是![]() 或
或![]() .
.
【答案】(1)不具备,理由见解析;(2)![]() 时,
时,![]() 且
且![]() ;
;![]() 时,
时,![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)先假设函数![]() 具有性质
具有性质![]() ,根据题意求出
,根据题意求出![]() ,与
,与![]() 矛盾,即可判断出结果;
矛盾,即可判断出结果;
(2)根据题意,得到![]() ,推出
,推出![]() ,求解,即可得出结果;
,求解,即可得出结果;
(3)根据题意,先得到![]() ,
,![]() ,根据等比数列的定义,以及数学归纳法,分别证明必要性和充分性,即可证明结论成立.
,根据等比数列的定义,以及数学归纳法,分别证明必要性和充分性,即可证明结论成立.
(1)若函数![]() 具有性质
具有性质![]() ;则
;则![]()
即![]() ,
,
所以![]() ,即
,即![]() ,与
,与![]() 矛盾,所以函数
矛盾,所以函数![]() 不具有性质
不具有性质![]() ;
;
(2)若函数![]() 具有性质
具有性质![]() ,
,
则![]() ,
,
即![]() ,
,
即![]() ,
,
所以![]() ,因此
,因此![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ;所以
;所以 ![]() 或
或![]() ;
;
当![]() 时,
时,![]() 且
且![]() ,所以
,所以![]() 且
且![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() ;
;
(3)因为函数![]() 在
在![]() 时具有性质
时具有性质![]() (其中
(其中![]() ,
,![]() ),
),
所以![]() ,
,
又函数![]() 不存在零点,
不存在零点,![]() ,
,
所以![]() ,
,![]() ;
;
下面证明必要性:
若数列![]() 为等比数列,则
为等比数列,则![]() ,
,
又![]() ,所以
,所以![]() ,
,
因此![]() ,所以
,所以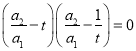 ,即
,即![]() 或
或![]() ;
;
接下来证明充分性:
若![]() ,因为
,因为![]() ,所以
,所以![]() ,因此
,因此![]() ;
;
猜想:![]() ;
;
用数学归纳法证明如下:
①当![]() 时,
时,![]() 显然成立;
显然成立;
②假设![]() 时,
时,![]() 成立,
成立,![]() 成立;
成立;
则当![]() 时,由
时,由![]() 得
得![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() ,
,
即![]() 时,
时,![]() 也成立,
也成立,
由①②可得,![]() 恒成立;即数列
恒成立;即数列![]() 为公比是
为公比是![]() 的等比数列;
的等比数列;
同理:![]() 时,数列
时,数列![]() 为公比是
为公比是![]() 的等比数列;
的等比数列;
综上,数列![]() 为等比数列的充要条件是
为等比数列的充要条件是![]() 或
或![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
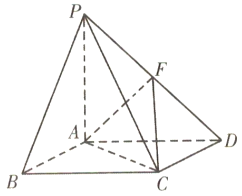
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为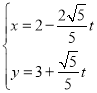 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)设点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且
上的点,且![]() .求
.求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】产量相同的机床一和机床二生产同一种零件,在一个小时内生产出的次品数分别记为![]() ,
,![]() ,它们的分布列分别如下:
,它们的分布列分别如下:
| 0 | 1 | 2 | 3 |
| 0.4 | 0.3 | 0.2 | 0.1 |
| 0 | 1 | 2 |
| 0.2 | 0.6 | 0.2 |
(1)哪台机床更好?请说明理由;
(2)记![]() 表示
表示![]() 台机床
台机床![]() 小时内共生产出的次品件数,求
小时内共生产出的次品件数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是边长为
是边长为![]() 的等边三角形,E、F分别为AB、AC的中点,
的等边三角形,E、F分别为AB、AC的中点,![]() ,沿EF把
,沿EF把![]() 折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥
折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥![]() 的外接球的表面积的最小值为________,此时四棱锥
的外接球的表面积的最小值为________,此时四棱锥![]() 的体积为________.
的体积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年是我国垃圾分类逐步凸显效果关键的一年.在国家高度重视,重拳出击的前提下,高强度、高频率的宣传教育能有效缩短我国生活垃圾分类走入世界前列所需的时间,打好垃圾分类这场“持久战”,“全民战”.某市做了一项调查,在一所城市中学和一所县城中学随机各抽取15名学生,对垃圾分类知识进行问答,满分为100分,他们所得成绩如下:
城市中学学生成绩分别为:73 71 83 86 92 70 88 93 73 97 87 88 74 86 85
县城中学学生成绩分别为:60 64 71 91 60 76 72 85 81 72 62 74 73 63 72

(1)根据上述两组数据在图中完成两所中学学生成绩的茎叶图,并通过茎叶图比较两所中学学生成绩的平均分及分散程度;(不要求计算出具体值,给出结论即可)
(2)从城市中学成绩在80分以上的学生中抽取4名,记这4名学生的成绩在90分以上的人数为X,求X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com