
【题目】2020年是我国垃圾分类逐步凸显效果关键的一年.在国家高度重视,重拳出击的前提下,高强度、高频率的宣传教育能有效缩短我国生活垃圾分类走入世界前列所需的时间,打好垃圾分类这场“持久战”,“全民战”.某市做了一项调查,在一所城市中学和一所县城中学随机各抽取15名学生,对垃圾分类知识进行问答,满分为100分,他们所得成绩如下:
城市中学学生成绩分别为:73 71 83 86 92 70 88 93 73 97 87 88 74 86 85
县城中学学生成绩分别为:60 64 71 91 60 76 72 85 81 72 62 74 73 63 72

(1)根据上述两组数据在图中完成两所中学学生成绩的茎叶图,并通过茎叶图比较两所中学学生成绩的平均分及分散程度;(不要求计算出具体值,给出结论即可)
(2)从城市中学成绩在80分以上的学生中抽取4名,记这4名学生的成绩在90分以上的人数为X,求X的分布列与数学期望.
【答案】(1)茎叶图见解析,城市中学的平均分高于县城中学平均分,城市中学学生成绩比较集中,县城中学学生成绩比较分散;(2)分布列见解析,![]() .
.
【解析】
(1)县城中学学生成绩60段有5人,70分段有7人,80分段2人,90分段1人,共四个分数段;城市中学学生成绩60段有0人,70分段有5人,80分段7人,90分段3人,共三个分数段;城市中学学生成绩平均分高一些,也相对集中.
(2)城市中学成绩 80分以上的学生共有10名,93分以上的学生共有3名, 从城市中学成绩在80分以上的学生中抽取4名,因此![]() ,1,2,3,由古典概型计算各个概率,列出分布列,后求期望即可.
,1,2,3,由古典概型计算各个概率,列出分布列,后求期望即可.
解:(1)茎叶图如图所示.

城市中学的平均分高于县城中学平均分,
城市中学学生成绩比较集中,县城中学学生成绩比较分散.
(2)80分以上的学生共有10名,93分以上的学生共有3名,
由题可知![]() ,1,2,3,
,1,2,3,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
X的分布列为
|
|
|
|
|
|
|
|
|
|
![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为D,若存在实常数
的定义域为D,若存在实常数![]() 及
及![]() ,对任意
,对任意![]() ,当
,当![]() 且
且![]() 时,都有
时,都有![]() 成立,则称函数
成立,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断函数![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)若函数![]() 具有性质
具有性质![]() ,求
,求![]() 及
及![]() 应满足的条件;
应满足的条件;
(3)已知函数![]() 不存在零点,当
不存在零点,当![]() 时具有性质
时具有性质![]() (其中
(其中![]() ,
,![]() ),记
),记![]() ,求证:数列
,求证:数列![]() 为等比数列的充要条件是
为等比数列的充要条件是![]() 或
或![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱柱ABC﹣A1B1C1中,E是棱AB的中点,动点F是侧面ACC1A1(包括边界)上一点,若EF//平面BCC1B1,则动点F的轨迹是( )
A.线段B.圆弧
C.椭圆的一部分D.抛物线的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当今世界科技迅猛发展,信息日新月异.为增强全民科技意识,提高公众科学素养,某市图书馆开展了以“亲近科技、畅想未来”为主题的系列活动,并对不同年龄借阅者对科技类图书的情况进行了调查.该图书馆从只借阅了一本图书的借阅者中随机抽取100名,数据统计如表:
借阅科技类图书(人) | 借阅非科技类图书(人) | |
年龄不超过50岁 | 20 | 25 |
年龄大于50岁 | 10 | 45 |
(1)是否有99%的把握认为年龄与借阅科技类图书有关?
(2)该图书馆为了鼓励市民借阅科技类图书,规定市民每借阅一本科技类图书奖励积分2分,每借阅一本非科技类图书奖励积分1分,积分累计一定数量可以用积分换购自己喜爱的图书.用表中的样本频率作为概率的估计值.
(i)现有3名借阅者每人借阅一本图书,记此3人增加的积分总和为随机变量ξ,求ξ的分布列和数学期望;
(ii)现从只借阅一本图书的借阅者中选取16人,则借阅科技类图书最有可能的人数是多少?
附:K2![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,P,Q,M,N,H,R是各条棱的中点.
中,P,Q,M,N,H,R是各条棱的中点.
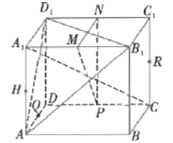
①直线![]() 平面
平面![]() ;②
;②![]() ;③P,Q,H,R四点共面;④
;③P,Q,H,R四点共面;④![]() 平面
平面![]() .其中正确的个数为( )
.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com