
【题目】已知![]() 是数列
是数列![]() 的前
的前![]() 项和,并且
项和,并且![]() ,对任意正整数
,对任意正整数![]() ,
, ![]() ,设
,设![]() (
(![]() ).
).
(1)证明:数列![]() 是等比数列,并求
是等比数列,并求![]() 的通项公式;
的通项公式;
(2)设![]() ,求证:数列
,求证:数列![]() 不可能为等比数列.
不可能为等比数列.
【答案】(1)答案见解析;(2)证明见解析.
【解析】试题分析:(1)利用an+1=Sn+1-Sn可知证明an+1=4(an-an-1),通过bn=an+1-2an可知bn+1=2(an+1-2an),通过作商可知{bn}是公比为2的等比数列,通过a1=1可知b1=3,进而可得结论;
(2)假设![]() 为等比数列,则有
为等比数列,则有![]() , n≥2, 则有
, n≥2, 则有![]() ,故假设不成立,则数列
,故假设不成立,则数列![]() 不可能为等比数列 .
不可能为等比数列 .
试题解析:(I)∵Sn+1=4an+2,∴Sn=4an-1+2(n≥2),
两式相减:an+1=4an-4an-1(n≥2),∴an+1=4(an-an-1)(n≥2),
∴bn=an+1-2an,
∴bn+1=an+2-2an+1=4(an+1-an)-2an+1,bn+1=2(an+1-2an)=2bn(n∈N*),
∴![]() ,∴{bn}是以2为公比的等比数列,
,∴{bn}是以2为公比的等比数列,
∵b1=a2-2a1,而a1+a2=4a1+2,∴a2=3a1+2=5,b1=5-2=3,
∴bn=32n-1(n∈N*)
(II)![]() ,假设
,假设![]() 为等比数列,则有
为等比数列,则有
![]()
![]()
![]()
![]() , n≥2, 则有
, n≥2, 则有![]() =0
=0
与![]() ≥1矛盾,所以假设不成立,则原结论成立,即
≥1矛盾,所以假设不成立,则原结论成立,即
数列![]() 不可能为等比数列
不可能为等比数列


科目:高中数学 来源: 题型:
【题目】一条光线经过P(2,3)点,射在直线l:x+y+1=0上,反射后穿过点Q(1,1).
(1)求入射光线的方程;
(2)求这条光线从P到Q的长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:

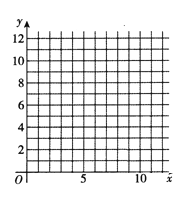
(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线![]() 的右下方的概率.
的右下方的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:三棱锥![]() 中,侧面
中,侧面![]() 垂直底面,
垂直底面, ![]() 是底面最长的边;图1是三棱锥
是底面最长的边;图1是三棱锥![]() 的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥
的三视图,其中的侧视图和俯视图均为直角三角形;图2是用斜二测画法画出的三棱锥![]() 的直观图的一部分,其中点
的直观图的一部分,其中点![]() 在
在![]() 平面内.
平面内.
(Ⅰ)请在图2中将三棱锥![]() 的直观图补充完整,并指出三棱锥
的直观图补充完整,并指出三棱锥![]() 的哪些面是直角三角形;
的哪些面是直角三角形;![]()
![]()
(Ⅱ)设二面角![]() 的大小为
的大小为![]() ,求
,求![]() 的值;
的值;
(Ⅲ)求点![]() 到面
到面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,且
,且![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() .
.
①求证: ![]() ;
;
②当![]() 为何值时,
为何值时, ![]() 取得最大值?并求出最大值.
取得最大值?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知与曲线![]() 相切的直线
相切的直线![]() ,与
,与![]() 轴,
轴, ![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为原点,
为原点, ![]() ,
, ![]() ,(
,( ![]() ).
).
(1)求证:: ![]() 与
与![]() 相切的条件是:
相切的条件是: ![]() .
.
(2)求线段![]() 中点的轨迹方程;
中点的轨迹方程;
(3)求三角形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图像如图所示,则下列结论中一定成立的是( )
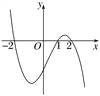
A. 函数f(x)有极大值f(2)和极小值f(1) B. 函数f(x)有极大值f(-2)和极小值f(1)
C. 函数f(x)有极大值f(2)和极小值f(-2) D. 函数f(x)有极大值f(-2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为研究患肺癌与是否吸烟有关,某肿瘤机构随机抽取了40人做相关调查,其中不吸烟人数与吸烟人数相同,已知吸烟人数中,患肺癌与不患肺癌的比为![]() ;不吸烟的人数中,患肺癌与不患肺癌的比为
;不吸烟的人数中,患肺癌与不患肺癌的比为![]() .
.
(1)现从患肺癌的人中用分层抽样的方法抽取5人,再从这5人中随机抽取2人进行调查,求这两人都是吸烟患肺癌的概率;
(2)是否有99.9%的把握认为患肺癌与吸烟有关?
附: 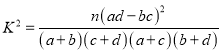 ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com