【题目】一条光线经过P(2,3)点,射在直线l:x＋y＋1＝0上,反射后穿过点Q(1,1).

(1)求入射光线的方程;

(2)求这条光线从P到Q的长度.

参考答案：

【答案】(1) 5x－4y＋2＝0. (2)

【解析】试题分析：（1）设点Q′（x′，y′）为Q关于直线l的对称点且QQ′交l于M点，可得直线QM的方程，与l联立可得点M的坐标，利用中点坐标公式可得Q′的坐标．设入射线与l交于点N，利用P，N，Q′共线，得到入射光线PN的方程；
（2）利用两点间的距离公式求出PQ′即可．

试题解析：

(1)设点Q′(x′,y′)为Q关于直线l的对称点且QQ′交l于M点.

∵,∴kQQ′＝1.

∴QQ′所在直线方程为y－1＝1·(x－1),

即x－y＝0.

由

解得l与QQ′的交点M的坐标为.

又∵M为QQ′的中点,

由此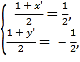得解得

∴Q′(－2,－2).

设入射光线与l交点为N,则P、N、Q′共线.

又P(2,3),Q′(－2,－2),得入射光线的方程为,

即5x－4y＋2＝0.

(2)∵l是QQ′的垂直平分线,从而|NQ|＝|NQ′|,

∴|PN|＋|NQ|＝|PN|＋|NQ′|＝|PQ′|＝,

即这条光线从P到Q的长度是.

关闭