练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某学校高二年级志愿者协会有6名男同学，4名女同学. 在这10名同学中，3名同学来自A班，其余7名同学恰好来自其他互不相同的七个班级. 现从这10名同学中随机选取3名同学，到某公园参加环保活动（每位同学被选到的可能性相同）.

    （Ⅰ）求选出的3名同学是来自互不相同班级的概率；

    （Ⅱ）设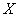为选出的3名同学中女同学的人数，求随机变量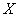的分布列和数学期望.


    解：设“选出的3名同学来自互不相同的学院”为事件，则

    .…………………………4分

    所以，选出的3名同学来自互不相同学院的概率为.…………………………5分

    （Ⅱ）解：随机变量的所有可能值为0，1，2，3.

    .…………………………9分

    所以，随机变量的分布列是

    0

    1

    2

    3

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知直线与椭圆相交于两个不同的点，记与轴的交点为．

    （Ⅰ）若，且，求实数的值；

    （Ⅱ）若，求面积的最大值，及此时椭圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的定义域为集合，函数的值域为集合．

    （Ⅰ）求集合，；

    （Ⅱ）已知命题：,命题：，若是的充分不必要条件，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    奇函数上为增函数,且,则不等式的解集为(     ).

    A              B．

    C．              D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从装有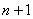个球（其中n个白球，1个黑球）的口袋中取出m个球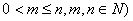（，共有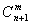种取法. 在这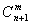种取法中，可以分成两类：一类是取出的m个球全部为白球，共有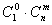种取法；另一类是取出的m个球有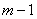个白球和1个黑球，共有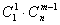种取法. 显然

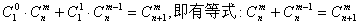    成立.

    试根据上述思想化简下列式子：

                     .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，假设正确的是（  ）

    A．假设三内角都不大于60度          B．假设三内角都大于60度

    C．假设三内角至多有一个大于60度    D． 假设三内角至多有两个大于60度

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数有（  ）

    A．极大值5，无极小值            B．极小值－27，无极大值

    C．极大值5，极小值－27          D．极大值5，极小值－11

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数．

    （Ⅰ）当时，求曲线在处的切线方程；

    （Ⅱ）设函数，求函数的单调区间；

    （Ⅲ）若，在上存在一点，使得成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数，，（）

    （1）问取何值时，方程在上有两解；

    （2）若对任意的，总存在，使成立，求实数的取值范围。

    查看答案和解析>>

    同步练习册答案