下列命题正确的有 (把所有正确命题的序号填在横线上):
①若数列{an}是等差数列,且am+an=as+at(m、n、s、t∈N*),则m+n=s+t;
②若Sn是等差数列{an}的前n项的和,则Sn,S2n-Sn,S3n-S2n成等差数列;
③若Sn是等比数列{an}的前n项的和,则Sn,S2n-Sn,S3n-S2n成等比数列;
④若Sn是等比数列{an}的前n项的和,且Sn=Aqn+B;(其中A、B是非零常数,n∈N*),则A+B为零.
【答案】
分析:①取数列{a
n}为常数列,即可推出该命题是假命题;②根据等差数列的性质,推出2(S
2n-S
n)=S
n+(S
3n-S
2n),即可得到S
n,S
2n-S
n,S
3n-S
2n,…为等差数列;③利用等比数列的特例判断选项是否正确;④根据数列的前n项的和减去第n-1项的和得到数列的第n项的通项公式,即可得到此等比数列的首项与公比,根据首项和公比,利用等比数列的前n项和的公式表示出前n项的和,与已知的S
n=3
n+b对比后,即可得到b的值.
解答:解:①取数列{a
n}为常数列,对任意m、n、s、t∈N*,都有a
m+a
n=a
s+a
t,故错;
②设等差数列a
n的首项为a
1,公差为d,
则S
n=a
1+a
2+…+a
n,S
2n-S
n=a
n+1+a
n+2+…+a
2n=a
1+nd+a
2+nd+…+a
n+nd=S
n+n
2d,
同理:S
3n-S
2n=a
2n+1+a
2n+2+…+a
3n=a
n+1+a
n+2+…+a
2n+n
2d=S
2n-S
n+n
2d,
∴2(S
2n-S
n)=S
n+(S
3n-S
2n),
∴S
n,S
2n-S
n,S
3n-S
2n是等差数列.此选项正确;
③设a
n=(-1)
n,
则S
2=0,S
4-S
2=0,S
6-S
4=0,
∴此数列不是等比数列,此选项错;
④因为a
n=S
n-S
n-1=(Aq
n+B)-(Aq
n-1+B)=Aq
n-Aq
n-1=(Aq-1)×q
n-1,
所以此数列为首项是Aq-1,公比为q的等比数列,
则S
n=
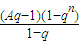
,
所以B=
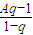
,A=-
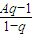
,∴A+B=0,故正确;
故答案为②④.
点评:此题考查学生灵活运用等差、等比数列的性质化简求值,是一道综合题.属中档题.

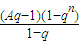 ,
,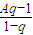 ,A=-
,A=-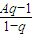 ,∴A+B=0,故正确;
,∴A+B=0,故正确;
