
【题目】已知函数![]() .
.
(1)若m=0,求函数f(x)的定义域;
(2)若函数f(x)的值域为R,求实数m的取值范围;
(3)若函数f(x)在区间![]() 上是增函数,求实数m的取值范围.
上是增函数,求实数m的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围是 ( ).
A. ![]() B.[-1,0] C.(-∞,-2] D.
B.[-1,0] C.(-∞,-2] D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,PA=AB=AD=2,四边形ABCD满足AB⊥AD,BC∥AD且BC=4,点M为PC的中点,点E为BC边上的点,且 ![]() =λ.
=λ. 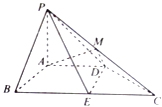
(1)求证:平面ADM⊥平面PBC;
(2)是否存在实数λ,使得二面角P﹣DE﹣B的余弦值为 ![]() ?若存在,求出实数λ的值,若不存在,请说明理由.
?若存在,求出实数λ的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() 满足:对任意的实数x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0成立,则实数a的取值范围是( )
满足:对任意的实数x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0成立,则实数a的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|2x-1≥1},B={x|x2-4x-5<0}.
(Ⅰ)求A∩B,(UA)∪(UB);
(Ⅱ)设集合C={x|m+1<x<2m-1},若B∩C=C,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方形![]() 的棱长为1,点
的棱长为1,点![]() 分别是棱
分别是棱![]() 的中点.
的中点.
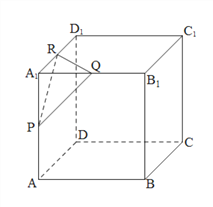
(Ⅰ)求二面角![]() 的余弦值;
的余弦值;
(Ⅱ)以![]() 为底面作正三棱柱,若此三棱柱另一底面三个顶点也都在该正方体的表面上,求这个正三棱柱的高.
为底面作正三棱柱,若此三棱柱另一底面三个顶点也都在该正方体的表面上,求这个正三棱柱的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品企业一个月内被消费者投诉的次数用![]() 表示.据统计,随机变量
表示.据统计,随机变量![]() 的概率分布如下表所示.
的概率分布如下表所示.
| 0 | 1 | 2 | 3 |
| 0.1 | 0.3 |
|
|
(1)求![]() 的值和
的值和![]() 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com