
设l、m是两条不同的直线,α、β是两个不同的平面,给出下列5个命题:
①若m⊥α,l⊥β,则l∥α;
②若m⊥α,l?β,l∥m,则α⊥β;
③若α∥β,l⊥α,m∥β,则l⊥m;
④若α∥β,l∥α,m?β,则l∥m;
⑤若α⊥β,α∩β=l,m⊥l,则m⊥β.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
B
【解析】
试题分析:根据空间面面垂直、平行的判定和性质,以及线面垂直、平行的判定与性质可以证出②③是真命题,而且①④⑤缺少条件,是假命题.由此可得本题的答案.
【解析】
对于①,m⊥α,l⊥β,没有指出平面α、β的位置关系,也没有指出m、l的位置关系,
因此不能确定l与α的位置关系,故①不正确;
对于②,由m⊥α,l∥m,得l⊥α,再结合l?β,可得α⊥β,故②正确;
对于③,由α∥β,l⊥α,得l⊥β,结合m∥β,可得l⊥m,故③正确;
对于④,由α∥β,l∥α,得l∥β或l?β,结合m?β,得l与m平行、相交或异面都有可能,故④不正确;
对于⑤,若α⊥β,α∩β=l,m⊥l,当m是α内的直线时有m⊥β,但条件中没有“m?α”这一条,
不一定有m⊥β,故⑤不正确.
因此正确命题为②③,共2个
故选B


科目:高中数学 来源:[同步]2015年人教B版必修二2.4 空间直角坐标系练习卷(解析版) 题型:选择题
若已知A(1,1,1),B(﹣3,﹣3,﹣3),则线段AB的长为( )
A.4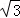 B.2
B.2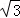 C.4
C.4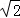 D.3
D.3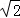
查看答案和解析>>
科目:高中数学 来源:[同步]2015年人教A版必修二4.3 空间直角坐标系练习卷(解析版) 题型:
已知空间三点的坐标为A(1,5,﹣2),B(2,4,1),C(p,3,q+2),若A,B,C三点共线,则p= ,q= .
查看答案和解析>>
科目:高中数学 来源:[同步]2015人教B版选修4-5 3.2用数学归纳法证明不等式练习卷(解析版) 题型:选择题
已知x∈R+,不等式x+ ≥2,x+
≥2,x+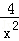 ≥3,…,可推广为x+
≥3,…,可推广为x+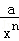 ≥n+1,则a的值为( )
≥n+1,则a的值为( )
A.2n B.n2 C.22(n﹣1) D.nn
查看答案和解析>>
科目:高中数学 来源:[同步]2015人教A版必修二2.1空间点、直线、平面间位置关系练习卷(解析版) 题型:
设a、b是两条不同的直线,α、β是两个不同的平面,则下列四个命题
①若a⊥b,a⊥α,则b∥α
②若a∥α,α⊥β,则a⊥β
③a⊥β,α⊥β,则a∥α
④若a⊥b,a⊥α,b⊥β,则α⊥β
其中正确的命题的个数是( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-6 2.3费马小定理和欧拉定理练习卷(解析版) 题型:解答题
证明:对任给的奇素数p,总存在无穷多个正整数n使得p|(n2n﹣1).
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-2 4.1变换的不变量 矩阵特征向量(解析版) 题型:填空题
(2014•闸北区三模)将正整数1,2,3,4,…,n2(n≥2)任意排成n行n列的数表.对于某一个数表,计算各行和各列中的任意两个数a,b(a>b)的比值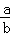 ,称这些比值中的最小值为这个数表的“特征值”.若aij表示某个n行n列数表中第i行第j列的数(1≤i≤n,1≤j≤n),且满足aij=
,称这些比值中的最小值为这个数表的“特征值”.若aij表示某个n行n列数表中第i行第j列的数(1≤i≤n,1≤j≤n),且满足aij=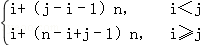 ,当n=4时数表的“特征值”为 .
,当n=4时数表的“特征值”为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
在直径为4的圆内接矩形中,最大的面积是( )
A.4 B.2 C.6 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com