
 的连续函数
的连续函数 ,对任意
,对任意 都有
都有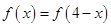 ,且其导函数
,且其导函数 满足
满足 ,则当
,则当 时,有( )
时,有( )A. | B. |
C.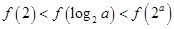 | D. |
科目:高中数学 来源:不详 题型:单选题
| A.10个 | B.9个 |
| C.8个 | D.7个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
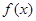 =
=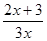 ,数列
,数列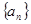 满足
满足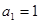 ,
,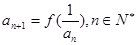 。(12分)
。(12分)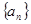 的通项公式;
的通项公式;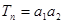 -
-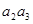 +
+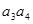 -
-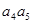 +…+
+…+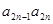 -
-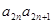 求
求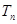 ;
;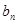 =
=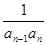 (
(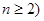 ,
,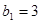 ,
,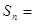
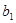 +
+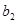 +
+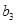 +┅
+┅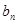 ,若
,若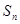 <
<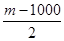 对一切
对一切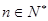 都成立,求最小的正整数
都成立,求最小的正整数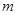 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
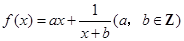 ,曲线
,曲线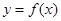 在点
在点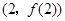 处的切线方程
处的切线方程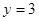 .
.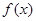 的解析式,并判断函数
的解析式,并判断函数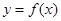 的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。
的图像是否为中心对称图形?若是,请求其对称中心;否则说明理由。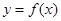 上任一点的切线与直线
上任一点的切线与直线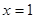 和直线
和直线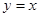 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.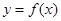 的图象向左平移一个单位后与抛物线
的图象向左平移一个单位后与抛物线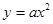 (
(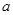 为非0常数)的图象有几个交点?(说明理由)
为非0常数)的图象有几个交点?(说明理由)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (万元)和
(万元)和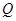 (万元),它们与投入资金
(万元),它们与投入资金 (万元)的关系有经验公式:
(万元)的关系有经验公式: 。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?
。今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得最大利润是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com