练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数y=-x3-x2+2，则（ ）
    A．有极大值，没有极小值
    B．有极小值，但无极大值
    C．既有极大值，又有极小值
    D．既无极大值，又无极小值
    【答案】分析：求导，令y′＞0，y′＜0求出函数y的单调区间，从而确定函数有无极值．
    解答：解：y′=-3x2-2x=-x（3x+2），令y′=0，x=0或x=
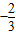
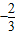
    令y′＞0得x＜或x＞0，令y′＜0得＜x＜0
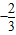
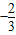
    ∴函数y在上[，0]是减函数，在（-∞，]，[0，+∞）是增函数
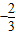
    ∴函数y在x=取得极大值，在x=0时取得极小值，
    故选C．
    点评：本题主要考查导数与极值的关系，若f（a）=0：a的左侧f'（x）＞0，a的右侧f'（x）＜0则a是极大值点；a的左侧f'（x）＜0，a的右侧f'（x）＞0则a是极小值点．属于基础知识，基本运算的考查．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数y=-x3-x2+2，则（　　）
    A、有极大值，没有极小值B、有极小值，但无极大值C、既有极大值，又有极小值D、既无极大值，又无极小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=x3-3x+d的图象与x轴恰有两个公共点，则d=
    ±2
    ±2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=x3-3x，则它的单调递减区间是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=x3-3x+c的图象与x轴恰有两个公共点，则c=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数y=x3+3ax2+3bx+c在x=2处有极值，且其图象在x=1处的切线与直线6x+2y+5=0平行．
    （1）求函数的单调区间；  
    （2）求函数的极大值与极小值的差．

    查看答案和解析>>

    同步练习册答案