
分析 由已知结合数列递推式可得数列{an}是周期为3的周期数列,由此可得前2011项的和.
解答 解:∵an+1•an=an+1-1,
∴${a}_{n}=1-\frac{1}{{a}_{n+1}}$,
∵a2011=2,∴${a}_{2010}=1-\frac{1}{{a}_{2011}}=1-\frac{1}{2}=\frac{1}{2}$,
${a}_{2009}=1-\frac{1}{{a}_{2010}}=1-\frac{1}{\frac{1}{2}}=-1$,
${a}_{2008}=1-\frac{1}{{a}_{2009}}=1-(-1)=2$,
…
∴数列{an}是周期为3的周期数列,
∵2011=670×3+1,
∴S2011=$(\frac{1}{2}+2-1)×670+2=1007$.
故答案为:1007.
点评 本题考查数列递推式,考查了等差数列的前n项和,寻找数列周期是关键,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{625}$ | B. | $\frac{96}{625}$ | C. | $\frac{624}{625}$ | D. | $\frac{4}{625}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
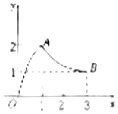 如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.
如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则$f[{\frac{1}{f(3)}}]$的值等于2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com