
已知矩形ABCD,AB=8,BC=6,按以下两种方法将其折叠为两部分,设两部分的面积为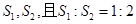 ,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.
,折痕为线段EF,问用哪一种方法折叠,折痕EF最长?并求EF长度的最大值.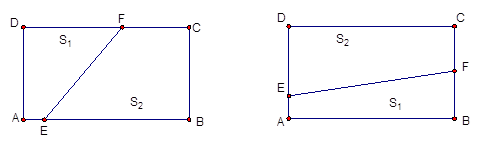
科目:高中数学 来源: 题型:解答题
某企业要建造一个容积为18m3,深为2m的长方体形无盖贮水池,如果池底和池壁每平方米的造价分别为200元和150元,怎样设计该水池可使得能总造价最低?最低总造价为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某化工企业2007年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备x年的年平均污水处理费用y(万元);
(2)为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点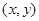 在△ABC内部,则
在△ABC内部,则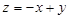 的取值范围是( )
的取值范围是( )
A.(1- ,2) ,2) | B.(0,2) | C.( -1,2) -1,2) | D.(0,1+ ) ) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com