
| f(x) |
| x |
| 1 |
| 2 |
| 3 |
| f(x) |
| x |
| lnx |
| x |
| 1 |
| x |
| lnx |
| x |
| 1 |
| x |
| 1 |
| 2 |
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| lnx |
| x |
| 1 |
| x |
| 1 |
| 2 |
| lnx |
| x |
| 1 |
| x |
| 1-lnx |
| x2 |
| 1 |
| x2 |
| x2-lnx |
| x2 |
| 1 |
| x |
| 2x2-1 |
| x |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| OA |
| OB |
| OA |
| OB |
| 2 |
| 3 |
| ab |
| 3 |
| 9 |
| ab |
| 36 |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| BF |
| FA |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
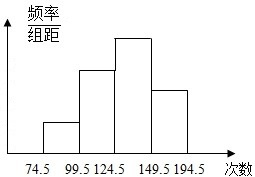 为了解学生的体能情况,抽取了一个学校的部分学生进行一分钟跳绳次数测试,将所得数据整理成统计图如图,已知图中从左到右各个小组的高度之比分别为1:3:4:2,最左边一组的频数为5,请根据以上信息和图形解决以下问题:
为了解学生的体能情况,抽取了一个学校的部分学生进行一分钟跳绳次数测试,将所得数据整理成统计图如图,已知图中从左到右各个小组的高度之比分别为1:3:4:2,最左边一组的频数为5,请根据以上信息和图形解决以下问题:查看答案和解析>>
科目:高中数学 来源: 题型:
|
| Sn |
| 3•2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
| a |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| ||
| 2 |
| π |
| 3 |
| π |
| 2 |
| 1 | ||
|
| 1 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 1 |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=6上,圆弧C1的圆心是坐标原点O,半径为10,圆弧C2过点A(38,0).
如图,在平面直角坐标系xOy中,已知曲线C由圆弧C1和圆弧C2相接而成,两相接点M、N均在直线x=6上,圆弧C1的圆心是坐标原点O,半径为10,圆弧C2过点A(38,0).| 39 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com