
【题目】已知正四棱柱ABCD﹣A1B1C1D1中,AA1=2AB,则CD与平面BDC1所成角的正弦值等于( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:设AB=1,则AA1=2,分别以 ![]() 的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,
的方向为x轴、y轴、z轴的正方向建立空间直角坐标系,
如下图所示: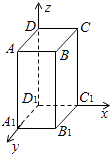
则D(0,0,2),C1(1,0,0),B(1,1,2),C(1,0,2),![]() =(1,1,0),
=(1,1,0), ![]() =(1,0,﹣2),
=(1,0,﹣2), ![]() =(1,0,0),
=(1,0,0),
设 ![]() =(x,y,z)为平面BDC1的一个法向量,则
=(x,y,z)为平面BDC1的一个法向量,则  ,即
,即 ![]() ,取
,取 ![]() =(2,﹣2,1),
=(2,﹣2,1),
设CD与平面BDC1所成角为θ,则sinθ=| 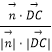 |=
|= ![]() ,
,
故选A.
【考点精析】通过灵活运用空间角的异面直线所成的角和用空间向量求直线与平面的夹角,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则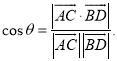 ;设直线
;设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: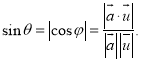 即可以解答此题.
即可以解答此题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共![]() 个,生产一个卫兵需
个,生产一个卫兵需![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润![]() 元.
元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间D上的函数f(x),若存在闭区间[a,b]D和常数c,使得对任意x1∈[a,b],都有f(x1)=c,且对任意x2∈D,当x2[a,b]时,f(x2)<c恒成立,则称函数f(x)为区间D上的“平顶型”函数.给出下列结论:
①“平顶型”函数在定义域内有最大值;
②函数f(x)=x-|x-2|为R上的“平顶型”函数;
③函数f(x)=sin x-|sin x|为R上的“平顶型”函数;
④当t≤![]() 时,函数f(x)=
时,函数f(x)= 是区间[0,+∞)上的“平顶型”函数.
是区间[0,+∞)上的“平顶型”函数.
其中正确的结论是________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD, ![]() .
.
(1)证明:A1C⊥平面BB1D1D; 
(2)求平面OCB1与平面BB1D1D的夹角θ的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com