Question

17．在△OAB中$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$分别为$\overrightarrow{OA}$、$\overrightarrow{OB}$上的单位向量，∠AOB=120°，|OA|=3，且（$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$）⊥$\overrightarrow{AB}$．
（1）判断△OAB的形状；
（2）求S_△OAB．

Answer 1

分析 （1）由题意$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$表示∠AOB的平分线，根据（$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$）⊥$\overrightarrow{AB}$．可得Rt△OAE≌Rt△BOE，从而可得OA=OB．
（2）利用三角形面积公式即可得解．

解答 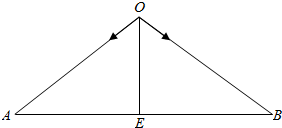解：（1）∵$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$分别为$\overrightarrow{OA}$、$\overrightarrow{OB}$上的单位向量，
∴$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$表示∠AOB的平分线，
∵（$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$）⊥$\overrightarrow{AB}$．
∴Rt△OAE≌Rt△BOE，
∴OA=OB，
∴△BOA是等腰三角形．
（2）S_△OAB=$\frac{1}{2}•$|$\overrightarrow{OA}$|•|$\overrightarrow{OB}$|•sin∠AOB
=$\frac{1}{2}×3×3×sin120°$
=$\frac{9\sqrt{3}}{4}$．

点评 本题主要考查了三角形的形状判断，平面向量数量积的运算，角平分线的性质，三角形面积公式的应用，属于基本知识的考查．