
分析 (1)利用椭圆的离心率e=$\frac{\sqrt{6}}{3}$,连接椭圆的四个顶点得到的菱形的面积为4$\sqrt{3}$,建立方程,求出a,b,即可求椭圆的方程;
(2)设出直线方程,将直线方程与椭圆方程联立,利用韦达定理得到交点的坐标满足的关系,利用向量垂直的充要条件列出等式,求出直线的斜率,即得到直线的方程.
解答 解:(1)∵椭圆的离心率e=$\frac{\sqrt{6}}{3}$,连接椭圆的四个顶点得到的菱形的面积为4$\sqrt{3}$,
∴$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,$\frac{1}{2}•2a•2b$=4$\sqrt{3}$,
∴a=$\sqrt{6}$,b=$\sqrt{2}$,
∴椭圆的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{2}=1$;
(2)设直线l的方程为y=k(x-3),P(x1,y1),Q(x2,y2).
由直线与椭圆方程联立可得(1+3k2)x2-18k2x+27k2-6=0.
∴x1+x2=$\frac{18{k}^{2}}{1+3{k}^{2}}$,x1x2=$\frac{27{k}^{2}-6}{1+3{k}^{2}}$
∵y1=k(x1-3),y2=k(x2-3),
∴y1y2=k2(x1-3)(x2-3)=$\frac{3{k}^{2}}{1+3{k}^{2}}$,
∵OP⊥OQ,∴y1y2+x1x2=0,
∴$\frac{27{k}^{2}-6}{1+3{k}^{2}}$+$\frac{3{k}^{2}}{1+3{k}^{2}}$=0
得k2=$\frac{1}{5}$,
此时△>0,∴k=±$\frac{\sqrt{5}}{5}$,
∴所求直线的方程为y=±$\frac{\sqrt{5}}{5}$(x-3).
点评 解决直线与圆锥曲线的位置关系的问题,一般将直线的方程与圆锥曲线方程联立,利用韦达定理找突破口.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 定义运算a*b为执行如图所示的程序框图输出的S值,则(sin$\frac{5π}{12}}$)*(${cos\frac{5π}{12}}$)的值为( )
定义运算a*b为执行如图所示的程序框图输出的S值,则(sin$\frac{5π}{12}}$)*(${cos\frac{5π}{12}}$)的值为( )| A. | $\frac{{2-\sqrt{3}}}{4}$ | B. | $\frac{{2+\sqrt{3}}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P4<1=P1=P2<P3=2 | B. | P1<1=P4=P2<P3=2 | C. | P4=1=P1=P2<P3=2 | D. | P4=1=P1<P2<P3=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
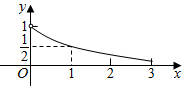 已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )
已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )| A. | 2x | B. | $-{(\frac{1}{2})^x}$ | C. | ${({\frac{1}{2}})^x}$ | D. | -2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1.70.2>0.73 | B. | lg3.4<lg2.9 | ||
| C. | log0.31.8<log0.32.7 | D. | 1.72>1.73 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,0) | C. | (0,$\frac{1}{4}$) | D. | ($\frac{1}{4}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com