
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
分析 (Ⅰ)求出每人选择贷款期限为12个月的概率,然后利用独立重复试验概率的乘法求解3人中恰有2人选择此贷款的概率.
(Ⅱ)求出享受补贴200元的概率为${P_1}=\frac{1}{5}$,享受补贴300元的概率为${P_2}=\frac{3}{5}$,享受补贴400元的概率为${P_3}=\frac{1}{5}$,即随机变量X的分布列,然后求解期望即可.
解答 (本小题满分12分)
解:(Ⅰ)由题意知,每人选择贷款期限为12个月的概率为$\frac{2}{5}$,(2分)
所以3人中恰有2人选择此贷款的概率为$P=C_3^2•{(\frac{2}{5})^2}•\frac{3}{5}=\frac{36}{125}$(6分)
(Ⅱ)由题意知,享受补贴200元的概率为${P_1}=\frac{1}{5}$,享受补贴300元的概率为${P_2}=\frac{3}{5}$,
享受补贴400元的概率为${P_3}=\frac{1}{5}$,即随机变量X的分布列为(9分)
| X | 200 | 300 | 400 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本小题主要考查学生对概率统计知识的理解,同时考查学生的数据处理能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
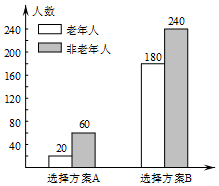 为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选出建设方案A和B向社会公开征集意见.有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下:
为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选出建设方案A和B向社会公开征集意见.有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下:| 选择方案A | 选择方案B | 总计 | |
| 老年人 | |||
| 非老年人 | |||
| 总计 | 500 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com