
【题目】(1)某圆锥的侧面展开图为圆心角为![]() ,面积为
,面积为![]() 的扇形,求该圆锥的表面积和体积.
的扇形,求该圆锥的表面积和体积.
(2)已知直三棱柱![]() 的底面是边长为
的底面是边长为![]() 的正三角形,且该三棱柱的外接球的表面积为
的正三角形,且该三棱柱的外接球的表面积为![]() ,求该三棱柱的体积.
,求该三棱柱的体积.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)设圆锥的底面半径、母线长分别为![]() ,利用扇形的面积公式求得
,利用扇形的面积公式求得![]() ,利用圆锥的表面积和体积公式,即可求解;
,利用圆锥的表面积和体积公式,即可求解;
(2)设球半径为![]() ,上,下底面中心设为
,上,下底面中心设为![]() ,由题意,外接球心为
,由题意,外接球心为![]() 的中点,根据三棱柱的外接球的表面积,列出方程,求得棱柱的高,利用体积公式,即可求解.
的中点,根据三棱柱的外接球的表面积,列出方程,求得棱柱的高,利用体积公式,即可求解.
(1)设圆锥的底面半径、母线长分别为![]() ,
,
则![]() ,解得
,解得![]()
所以圆锥的高为![]() ,得表面积是
,得表面积是![]() ,体积是
,体积是![]()
(2)设球半径为R,上,下底面中心设为M,N,由题意,外接球心为MN的中点,
设为O,则OA=R,由4πR2=12π,得R=OA=![]() ,又易得AM=
,又易得AM=![]() ,
,
由勾股定理可知,OM=1,所以MN=2,即棱柱的高h=2,
所以该三棱柱的体积为![]() .
.


科目:高中数学 来源: 题型:
【题目】2013年1月,北京经历了59年来雾霾天气最多的一个月.据气象局统计,北京市2013年1月1日至1月30日这30天里有26天出现雾霾天气,《环境空气质量指数(AQI)技术规定(试行)》如表1:
表1 空气质量指数AQI分组表
AQI指数M | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
级别 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
表2是某气象观测点记录的连续4天里AQI指数M与当天的空气水平可见度y(km)的情况,表3是某气象观测点记录的北京市2013年1月1日至1月30日的AQI指数频数分布表.
表2 AQI指数M与当天的空气水平可见度y(km)的情况
AQI指数M | 900 | 700 | 300 | 100 |
空气水平可见度y(km) | 0.5 | 3.5 | 6.5 | 9.5 |
表3 北京市2013年1月1日至1月30日AQI指数频数分布表
AQI指数M | [0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设x=![]() ,根据表2的数据,求出y关于x的线性回归方程.
,根据表2的数据,求出y关于x的线性回归方程.
(参考公式: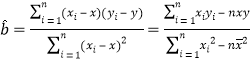 ,
,![]() .)
.)
(2)小王在北京开了一家洗车店,经小王统计:当AQI指数低于200时,洗车店平均每天亏损约2000元;当AQI指数在200至400时,洗车店平均每天收入约4000元;当AQI指数不低于400时,洗车店平均每天收入约7000元.
①估计小王的洗车店在2013年1月份平均每天的收入;
②从AQI指数在[0,200)和[800,1000]内的这6天中抽取2天,求这2天的收入之和不低于5000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C: ![]() +y2=1上,过M做x轴的垂线,垂足为N,点P满足
+y2=1上,过M做x轴的垂线,垂足为N,点P满足 ![]() =
= ![]() .
.
(Ⅰ)求点P的轨迹方程;
(Ⅱ)设点Q在直线x=﹣3上,且 ![]()
![]() =1.证明:过点P且垂直于OQ的直线l过C的左焦点F.
=1.证明:过点P且垂直于OQ的直线l过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示.为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有![]() 米.若行车道总宽度
米.若行车道总宽度![]() 为
为![]() 米.
米.
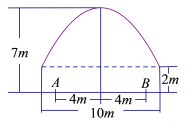
(1)计算车辆通过隧道时的限制高度;
(2)现有一辆载重汽车宽![]() 米,高
米,高![]() 米,试判断该车能否安全通过隧道?
米,试判断该车能否安全通过隧道?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cosx,C2:y=sin(2x+ ![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 ![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 ![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移 ![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的 ![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移 ![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]() 的离心率为
的离心率为![]() ,过椭圆右焦点
,过椭圆右焦点![]() 作两条互相垂直的弦
作两条互相垂直的弦![]() 与
与![]() .当直线
.当直线![]() 斜率为0时,
斜率为0时,![]() .
.
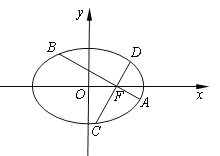
(1)求椭圆的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A.1盏
B.3盏
C.5盏
D.9盏
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com