
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
分析 根据向量的数量积的运算法则计算即可.
解答 解:因为$(\overrightarrow a+2\overrightarrow b)•\overrightarrow a=3$,
所以${\overrightarrow a^2}+2\overrightarrow b•\overrightarrow a=3$,
所以${|{\overrightarrow a}|^2}+2|{\overrightarrow b}|•|{\overrightarrow a}|cos\frac{π}{3}=3$,
所以${1^2}+2×|{\overrightarrow b}|×1×\frac{1}{2}=3$,
所以$|{\overrightarrow b}|$=2.
故选:C
点评 本题考查向量的数量积公式,以及培养了学生的运算能力和转化能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
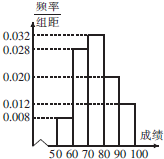 博鳌亚洲论坛2015年会员大会于3月27日在海南博鳌举办,大会组织者对招募的100名服务志愿者培训后,组织一次APEC知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.
博鳌亚洲论坛2015年会员大会于3月27日在海南博鳌举办,大会组织者对招募的100名服务志愿者培训后,组织一次APEC知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | $\frac{16}{3}$π | C. | 6π | D. | $\frac{20}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
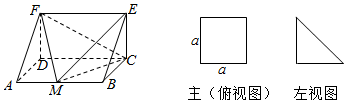 一个多面体的直观图和三视图如图所示,点M是边AB上的动点,记四面体E-FMC的体积为V1,多面体ADF-BCE的体积为V2,则$\frac{V_1}{V_2}$=( )
一个多面体的直观图和三视图如图所示,点M是边AB上的动点,记四面体E-FMC的体积为V1,多面体ADF-BCE的体积为V2,则$\frac{V_1}{V_2}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | ||
| C. | $\frac{1}{2}$ | D. | 不是定值,随点M的变化而变化 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com